To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
AbsorbanceIn spectroscopy, the absorbance A is defined as
Additional recommended knowledgewhere I is the intensity of light at a specified wavelength λ that has passed through a sample (transmitted light intensity) and I0 is the intensity of the light before it enters the sample or incident light intensity. Absorbance measurements are often carried out in analytical chemistry, since the absorbance of a sample is proportional to the thickness of the sample and the concentration of the absorbing species in the sample, in contrast to the transmittance I / I0 of a sample, which varies exponentially with thickness and concentration. See the Beer-Lambert law for a more complete discussion. ExplanationThe term absorption refers to the physical process of absorbing light, while absorbance refers to the mathematical quantity. Also, absorbance does not always measure absorption: if a given sample is, for example, a dispersion, part of the incident light will in fact be scattered by the dispersed particles, and not really absorbed. Absorbance only contemplates the ratio of transmitted light over incident light, not the mechanism by which light intensity decreases. Despite this fact, absorbance can still be used to determine concentrations (of particles) in such cases. Outside the field of analytical chemistry, the absorbance is sometimes defined as the natural logarithm instead of the base-10 logarithm. Although absorbance does not have true units, it is quite often reported in "Absorbance Units" or AU. Instrument Measurement rangeAny real measuring instrument has a limited range over which it can accurately measure absorbance. An instrument must be calibrated and checked against known standards if the readings are to be trusted. Many instruments will become non-linear (fail to follow the Beer-Lambert law) starting at approximately 2 AU (~1% Transmission). It is also difficult to accurately measure very small absorbances that are very close to zero absorbance. The theoretical best accuracy for most instruments is in the range near 1 AU. When possible, the path length or concentration should be adjusted to achieve readings near this range. It is extremely difficult to achieve a large instrument range, between 0 and 6 AU. Optical density, or OD, is the absorbance per unit length, i.e., the absorbance divided by the thickness of the sample, although it is sometimes used as a synonym for the absorbance with a base-10 logarithm. See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Absorbance". A list of authors is available in Wikipedia. |


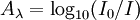 ,
,





