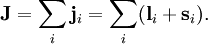To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Angular momentum coupling
Additional recommended knowledge
General theory and detailed originAngular momentum is a property of a physical system that is a constant of motion[1] (is time-independent and well-defined) in two situations: (i) The system experiences a spherical symmetric potential field. (ii) The system moves (in quantum mechanical sense) in isotropic space. In both cases the angular momentum operator commutes with the Hamiltonian of the system. By Heisenberg's uncertainty relation this means that the angular momentum can assume a sharp value simultaneously with the energy (eigenvalue of the Hamiltonian). An example of the first situation is an atom whose electrons only feel the Coulomb field of its nucleus. If we ignore the electron-electron interaction (and other small interactions such as spin-orbit coupling), the orbital angular momentum l of each electron commutes with the total Hamiltonian. In this model the atomic Hamiltonian is a sum of kinetic energies of the electrons and the spherical symmetric electron-nucleus interactions. The individual electron angular momenta l(i) commute with this Hamiltonian. That is, they are conserved properties of this approximate model of the atom. An example of the second situation is a rigid rotor moving in field-free space. A rigid rotor has a well-defined, time-independent, angular momentum. These two situations originate in classical mechanics. The third kind of conserved angular momentum, associated with spin, does not have a classical counterpart. However, all rules of angular momentum coupling apply to spin as well. In general the conservation of angular momentum implies full rotational symmetry (described by the groups SO(3) and SU(2)) and, conversely, spherical symmetry implies conservation of angular momentum. If two or more physical systems have conserved angular momenta, it can be useful to add these momenta to a total angular momentum of the combined system—a conserved property of the total system. The building of eigenstates of the total conserved angular momentum from the angular momentum eigenstates of the individual subsystems is referred to as angular momentum coupling. Application of angular momentum coupling is useful when there is an interaction between subsystems that, without interaction, would have conserved angular momentum. By the very interaction the spherical symmetry of the subsystems is broken, but the angular momentum of the total system remains a constant of motion. Use of the latter fact is helpful in the solution of the Schrödinger equation. As an example we consider two electrons, 1 and 2, in an atom (say the helium atom). If there is no electron-electron interaction, but only electron nucleus interaction, the two electrons can be rotated around the nucleus independently of each other; nothing happens to their energy. Both operators, l(1) and l(2), are conserved. However, if we switch on the electron-electron interaction depending on the distance d(1,2) between the electrons, then only a simultaneous and equal rotation of the two electrons will leave d(1,2) invariant. In such a case neither l(1) nor l(2) is a constant of motion but L = l(1) + l(2) is. Given eigenstates of l(1) and l(2), the construction of eigenstates of L (which still is conserved) is the coupling of the angular momenta of electron 1 and 2. In quantum mechanics, coupling also exists between angular momenta belonging to different Hilbert spaces of a single object, e.g. its spin and its orbital angular momentum. Reiterating slightly differently the above: one expands the quantum states of composed systems (i.e. made of subunits like two hydrogen atoms or two electrons) in basis sets which are made of direct products of quantum states which in turn describe the subsystems individually. We assume that the states of the subsystems can be chosen as eigenstates of their angular momentum operators (and of their component along any arbitrary z axis). The subsystems are therefore correctly described by a set of l, m quantum numbers (see angular momentum for details). When there is interaction between the subsystems, the total Hamiltonian contains terms that do not commute with the angular operators acting on the subsystems only. However, these terms do commute with the total angular momentum operator. Sometimes one refers to the non-commuting interaction terms in the Hamiltonian as angular momentum coupling terms, because they necessitate the angular momentum coupling. Footnote
Spin-orbit couplingThe behavior of atoms and smaller particles is well described by the theory of quantum mechanics, in which each particle has an intrinsic angular momentum called spin and specific configurations (of e.g. electrons in an atom) are described by a set of quantum numbers. Collections of particles also have angular momenta and corresponding quantum numbers, and under different circumstances the angular momenta of the parts add in different ways to form the angular momentum of the whole. Angular momentum coupling is a category including some of the ways that subatomic particles can interact with each other. In atomic physics, spin-orbit coupling also known as spin-pairing describes a weak magnetic interaction, or coupling, of the particle spin and the orbital motion of this particle, e.g. the electron spin and its motion around an atomic nucleus. One of its effects is to separate the energy of internal states of the atom, e.g. spin-aligned and spin-antialigned that would otherwise be identical in energy. This interaction is responsible for many of the details of atomic structure. In the macroscopic world of orbital mechanics, the term spin-orbit coupling is sometimes used in the same sense as spin-orbital resonance. LS couplingIn light atoms (generally Z<30), electron spins si interact among themselves so they combine to form a total spin angular momentum S. The same happens with orbital angular momenta li, forming a single orbital angular momentum L. The interaction between the quantum numbers L and S is called Russell-Saunders coupling or LS coupling. Then S and L add together and form a total angular momentum J:
This is an approximation which is good as long as any external magnetic fields are weak. In larger magnetic fields, these two momenta decouple, giving rise to a different splitting pattern in the energy levels (the Paschen-Back effect.), and the size of LS coupling term becomes small. For an extensive example on how LS-coupling is practically applied, see the article on Term symbols. jj couplingIn heavier atoms the situation is different. In atoms with bigger nuclear charges, spin-orbit interactions are frequently as large or larger than spin-spin interactions or orbit-orbit interactions. In this situation, each orbital angular momentum li tends to combine with each individual spin angular momentum si, originating individual total angular momenta ji. These then add up to form the total angular momentum J This description, facilitating calculation of this kind of interaction, is known as jj coupling. Spin-spin couplingSee also: J-coupling and Dipolar coupling in NMR spectroscopy Spin-spin coupling is the coupling of the intrinsic angular momentum (spin) of different particles. Such coupling between pairs of nuclear spins is an important feature of Nuclear Magnetic Resonance spectroscopy as it can provide detailed information about the structure and conformation of molecules. Spin-spin coupling between nuclear spin and electronic spin is responsible for hyperfine structure in atomic spectra. Term symbolsTerm symbols are used to represent the states and spectral transitions of atoms, they are found from coupling of angular momenta mentioned above. When the state of an atom has been specified with a term symbol, the allowed transitions can be found through selection rules by considering which transitions would conserve angular momentum. A photon has spin 1, and when there is a transition with emission or absorption of a photon the atom will need to change state to conserve angular momentum. The term symbol selection rules are. ΔS=0, ΔL=0,±1, Δl=±1, ΔJ=0,±1 Relativistic effectsIn very heavy atoms, relativistic shifting of the energies of the electron energy levels accentuates spin-orbit coupling effect. Thus, for example, uranium molecular orbital diagrams must directly incorporate relativistic symbols when considering interactions with other atoms. Nuclear couplingIn atomic nuclei, the spin-orbit interaction is much stronger than for atomic electrons, and is incorporated directly into the nuclear shell model. In addition, unlike atomic-electron term symbols, the lowest energy state is not L - S, but rather, l + s. All nuclear levels whose l value (orbital angular momentum) is greater than zero are thus split in the shell model to create states designated by l + s and l - s. Due to the nature of the shell model, which assumes an average potential rather than a central Coulombic potential, the nucleons that go into the l + s and l - s nuclear states are considered degenerate within each orbital (e.g. The 2p3/2 contains four nucleons, all of the same energy. Higher in energy is the 2p1/2 which contains two equal-energy nucleons). See alsoClebsch-Gordan coefficients |
||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Angular_momentum_coupling". A list of authors is available in Wikipedia. |





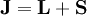 where
where 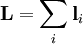 and
and