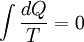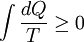Disgregation

In the history of thermodynamics, disgregation was defined in 1862 by Rudolf Clausius as the magnitude of the degree in which the molecules of a body are separated from each other.^[1] This term was modeled on certain passages in French physicist Sadi Carnot's 1824 paper On the Motive Power of Fire that characterized the "transformations" of "working substances" (particles of a thermodynamic system) of an engine cycle, namely "mode of aggregation", which was a precursor to the concept of entropy, which Clausius coined in 1865. It was also a precursor to that of Ludwig Boltzmann's 1870s theories of entropy and order and disorder.

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

Better weighing performance in 6 easy steps

Daily Visual Balance Check

Overview

In 1824, French physicist Sadi Carnot assumed that heat, like a substance, cannot be diminished in quantity and that it cannot increase. Specifically, he states that in a complete engine cycle ‘that when a body has experienced any changes, and when after a certain number of transformations it returns to its precisely its original state, that is, to that state considered in respect to density, to temperature, to mode of aggregation, let us suppose, I say that this body is found to contain the same quantity of heat that it contained at first, or else that the quantities of heat absorbed or set free in these different transformations are exactly compensated.’ Furthermore, he states that ‘this fact has never been called into question’ and ‘to deny this would overthrow the whole theory of heat to which it serves as a basis.’ This famous sentence, which Clausius spent fifteen years thinking about, marks the start of thermodynamics and signals the slow transition from the older caloric theory to the newer kinetic theory, in which heat is a type of energy in transit

In 1862, Clausius defined what is now known as entropy or the energetic effects related to irreversibility as the “equivalence-values of transformations” in a thermodynamic cycle. Clausius then signifies the difference between “reversible” (ideal) and “irreversible” (real) processes:

Equivalence-values of transformations

He then states what he calls the “theorem respecting the equivalence-values of the transformations” or what is now known as the second law of thermodynamics, as such:

Quantitatively, Clausius states the mathematical expression for this theorem is as follows. Let dQ be an element of the heat given up by the body to any reservoir of heat during its own changes, heat which it may absorb from a reservoir being here reckoned as negative, and T the absolute temperature of the body at the moment of giving up this heat, then the equation:

must be true for every reversible cyclical process, and the relation:

must hold good for every cyclical process which is in any way possible.

Verbal justifications

Clausius then points out the inherent difficulty in the mental comprehension of this law by stating: "although the necessity of this theorem admits of strict mathematical proof if we start from the fundamental proposition above quoted, it thereby nevertheless retains an abstract form, in which it is with difficulty embraced by the mind, and we feel compelled to seek for the precise physical cause, of which this theorem is a consequence." The justification for this law, according to Clausius, is based on the following argument:

To elaborate on this, Clausius states that in all cases in which heat can perform mechanical work, these processes always admit to being reduced to the “alteration in some way or another of the arrangement of the constituent parts of the body.” To exemplify this, Clausius moves into a discussion of change of state of a body, i.e. solid, liquid, gas. For instance, he states, “when bodies are expanded by heat, their molecules being thus separated from each other: in this case the mutual attractions of the molecules on the one hand, and external opposing forces on the other, insofar as any such are in operation, have to be overcome. Again, the state of aggregation of bodies is altered by heat, solid bodies rendered liquid, and both solid and liquid bodies being rendered aeriform: here likewise internal forces, and in general external forces also, have to be overcome.”

Definition of term

Clausius then goes on to introduce the term “disgregation”:

Ice melting

  Clausius then discusses the example of the melting of ice, a classic example which is used in almost all chemistry books to this day, and shows how we might represent the mechanical equivalent of work related to this energetic change mathematically:

Measurements of disgregation

As it is difficult to obtain direct measures of the interior forces that the molecules of the body exert on each other, Clausius states that an indirect way to obtain quantitative measures of what is now called entropy is to calculate the work done in overcoming internal forces:

In the case of the interior forces, it would accordingly be difficult—even if we did not want to measure them, but only to represent them mathematically—to find a fitting expression for them which would admit of a simple determination of the magnitude. This difficulty, however, disappears if we take into calculation, not the forces themselves, but the mechanical work which, in any change of arrangement, is required to overcome them. The expressions for the quantities of work are simpler than those for the corresponding forces; for the quantities of work can be all expressed, without further secondary statements, by the numbers which, having reference to the same unit, can be added together, or subtracted from one another, however various the forces may be to which they refer.

It is therefore convenient to alter the form of the above law by introducing, instead of the forces themselves, the work done in overcoming them. In this form it reads as follows:

This description is an early formulation of the concept of entropy.

References

1. ^ Clausius, Rudolf. (1862). "On the Application of the Theorem of the Equivalence of Transformations to Interior Work." Communicated to the Naturforschende Gesellschaft of Zurich, Jan. 27th, 1862; published in the Viertaljahrschrift of this Society, vol. vii. P. 48; in Poggendorff’s Annalen, May 1862, vol. cxvi. p. 73; in the Philosophical Magazine, S. 4. vol. xxiv. pp. 81, 201; and in the Journal des Mathematiques of Paris, S. 2. vol. vii. P. 209.