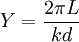To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Double-slit experiment
In the double-slit experiment, light is shone at a solid thin plate that has two slits cut into it. A photographic plate is set up to record what comes through those slits. One or the other slit may be open, or both may be open. When only one slit is open, the pattern on the plate is a diffraction pattern, a fairly narrow central band and dimmer bands parallel to it on each side. When both slits are open, the pattern displayed becomes very much more detailed and at least four times as wide. When two slits are open, probability wave fronts[1] emerge simultaneously from each slit and radiate in concentric circles. When the detector screen is reached the sum of the two probability wave fronts at each point determines the probability that a photon will be observed at that point. The end result when many photons are directed at the screen is a series of bands as pictured above. The interference of probability wave fronts is shown in the graph below. When two slits are open, but something is added to the experiment to allow a determination that a photon has passed through one or the other slit, then the interference pattern disappears and the experimental apparatus behaves yields two simple patterns, one from each slit. (See below.) The most baffling part of this experiment comes when only one photon at a time is fired at the barrier with both slits open. The pattern of interference remains the same as can be seen if many photons are emitted one at a time and recorded on the same sheet of photographic film. The clear implication is that something with a wavelike nature passes simultaneously through both slits and interferes with itself — even though there is only one photon present. (The experiment works with electrons, atoms, and even some molecules too.) "Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment."[2] Additional recommended knowledge
The underpinning of this experiment
Christiaan Huygens understood the basic idea of how light propagates and how to predict its path through a physical apparatus. He understood a light source to emit a series of waves comparable to the way that water waves spread out from something like a bobber that is jiggled up and down as it floats on the water surface. He said that the way to predict where the next wave front will be found is to generate a series of concentric circles on a sufficiently large number of points on a known wave front and then draw a curve that will pass tangent to all the resulting circles out in front of the known wave front. The diagram given here shows what happens when a flat wave front is extended in this manner, and what happens when a curved wave front is extended in the same way. Augustin Fresnel (1788-1827) based his proof that the wave nature of light does not contradict the observed fact that light propagates in a straight line in homogeneous media on Huygens' work, and also based himself on Huygens' ideas to give a complete account of diffraction and interference phenomena known at his time.[3] See the article Huygens–Fresnel principle for more information. The second drawing shows what happens when a flat wave front encounters a slit in a wall. Following the same principle elucidated above, it is clear that the new wave front will "bulge out" from the slit and light will be experienced as having diverged around the edges of the slit. The third drawing shows the explanation for interference based on the classical idea of a single wave front that represents all the light energy emitted by a source at one moment. Since photons diverge beyond the barrier wall, the distance between parts of any pattern they form on the target wall increase as the distance they have to travel increases, a fact that is well known from everyday experience with things like automobile headlights whose beams are not parallel. But decreasing the distance between slits will also increase the distance between fringes. Increasing the wavelength will also increase the distance between fringes as long as the slits are wide enough to permit the passage of light of that wavelength. Slits that are very wide in comparison to the frequency of the photons involved (e.g., two ordinary windows in a single wall) will permit light to appear to go "straight through." When light came to be understood as the result of electrons falling from higher energy orbits to lower energy orbits, the light that is delivered to some surface in any short interval of time came to be understood as ordinarily representing the arrival of very many photons, each with its own wave front. In understanding what actually happens in the two-slit experiment it became important to find out what happens when photons are emitted one by one.[5] When it became possible to perform that experiment, it became apparent that a single photon has its own wave front that passes through both slits, and that the single photon will show up on the detector screen according to probability values. When a great number of photons are sent through the apparatus one by one and recorded on photographic film, the same interference pattern emerges that had been seen before when many photons were being emitted at the same time. The double-slit experiment was first performed by Taylor in 1909,[6] by reducing the level of incident light until on average only one photon was being transmitted at a time.[7] Importance to physicsAlthough the double-slit experiment is now often referred to in the context of quantum mechanics, it is generally thought to have been first performed by the English scientist Thomas Young in the year 1801 in an attempt to resolve the question of whether light was composed of particles (Newton's "corpuscular" theory), or rather consisted of waves traveling through some ether, just as sound waves travel in air. The interference patterns observed in the experiment seemed to discredit the corpuscular theory, and the wave theory of light remained well accepted until the early 20th century, when evidence began to accumulate which seemed instead to confirm the particle theory of light.[8] The double-slit experiment, and its variations, then became a classic Gedanken experiment (thought experiment) for its clarity in expressing the central puzzles of quantum mechanics; although in this form the experiment was not actually performed with anything other than light until 1961, when Claus Jönsson of the University of Tübingen performed it with electrons[9][10], and not until 1974 in the form of "one electron at a time", in a laboratory at the University of Milan, by researchers led by Pier Giorgio Merli, of LAMEL-CNR Bologna. The results of the 1974 experiment were published and even made into a short film, but did not receive wide attention. The experiment was repeated in 1989 by Tonomura et al at Hitachi in Japan. Their equipment was better, reflecting 15 years of advances in electronics and a dedicated development effort by the Hitachi team. Their methodology was more precise and elegant, and their results agreed with the results of Merli's team. Although Tonomura asserted that the Italian experiment had not detected electrons one at a time—a key to demonstrating the wave-particle paradox—single electron detection is clearly visible in the photos and film taken by Merli and his group. In September 2002, the double-slit experiment of Claus Jönsson was voted "the most beautiful experiment" by readers of Physics World.[11] Importance to philosophyPhilosophy is concerned with the nature of our ideas about the world or worlds that each of us experience, how those ideas are grounded, and how to ferret out self-contradictions. The double-slit experiment is of great interest therefore, because it forces philosophers to reevaluate their ideas about such basic concepts as "particles,"[12] "waves," "location," "movement from one place to another," etc. In contrast to our way of conceptualizing the macro world of everyday experience, attempting to describe the motion of a single photon is problematic. As Philipp Frank observes, if we begin by investigating the motion of single particles through a single slit we can obtain a description of the pattern of photon strikes on a target screen. However, "the pattern of fringes for two slits is not the superposition of the two patterns for single slits. Hence, there is no law of motion that would determine the trajectory of a single photon and allow us to derive the observed facts that occur when photons pass two slits."[13] Experience in the micro world of sub-atomic particles forces us to reconceptualize some of our most commonplace ideas. One of the most striking consequences of the new science is that it is not in agreement with the belief of Laplace that an omniscient entity, knowing the initial positions and velocities of all particles in the universe at one time, could predict their positions at any future time. (To paraphrase Laplace's position, the positions and velocities of all things at any given time depend absolutely on their previous positions and velocities and the absolute laws that govern physical interactions.) Laplace believed that such particles would follow the laws of motion discovered by Newton, but twentieth century physics made it clear that the motions of sub-atomic particles and even some small atoms cannot be predicted by using the laws of Newtonian physics.[14] For instance, most of the orbits for electrons moving around atomic nuclei that are permitted by Newtonian physics are excluded by the new physics. And it is not even clear what the "movement" of a particle such as a photon may be when it is not clear that it "goes through" either one slit or the other, but it is clear that the probability of its arrival at various points on the target screen is a function of its wavelength and of the distance between the slits. Whereas Laplace would expect an omniscient spirit to be able to predict with absolute confidence the arrival of a photon at some specific point on the target screen, it turns out that the particle may arrive at one of a great number of points, but that the percentage of particles that arrive at each of such points is determined by the laws of the new physics. Results observedThe bright bands observed on the screen happen when the light has interfered constructively—where a crest of a wave meets a crest from another wave. The dark regions show destructive interference—a crest meets a trough. Constructive interference occurs when
This is only an approximation and depends on certain conditions.[16] It is possible to work out the wavelength of light using this equation and the above apparatus. If b and L are known and x is observed, then λ can be easily calculated. A detailed treatment of the mathematics of double-slit interference in the context of quantum mechanics is given in the article on Englert-Greenberger duality. Shape of interference fringesThe theoretical shapes of the interference fringes observed in Young's double slit experiment are straight lines which is easily proved. In case two pinholes are used instead of slits, as in the original Young's experiment, hyperbolic fringes are observed. If the two sources are placed on a line perpendicular to the screen, the shape of the interference fringes is circular as the individual paths travelled by light from the two sources are always equal for a given fringe. This can be done in simpler way by placing a mirror parallel to a screen at a distance and a source of light just above the mirror. (Note the extra phase difference of π due to reflection at the interface of a denser medium) Quantum version of experimentBy the 1920s, various other experiments (such as the photoelectric effect) had demonstrated that light interacts with matter only in discrete, "quantum"-sized packets called photons. If sunlight is replaced with a light source that is capable of producing just one photon at a time, and the screen is sensitive enough to detect a single photon, Young's experiment can, in theory, be performed one photon at a time with identical results. If either slit is covered, the individual photons hitting the screen, over time, create an ordinary diffraction pattern. But if both slits are left open, the pattern of photons hitting the screen, over time, again becomes a series of light and dark fringes. This result seems to both confirm and contradict the wave theory. If light were not to behave like a wave, there would be no interference pattern. On the other hand, if light were actually a wave then light energy would not arrive in discrete quantities (quanta) and would be spread over more space the farther the detector screen was placed from the screen with the slits in it. A remarkable result follows from a variation of the double-slit experiment in which detectors are placed in either or both of the two slits in an attempt to determine which slit the photon passes through on its way to the screen. Placing a detector even in just one of the slits will result in the disappearance of the interference pattern. The detection of a photon involves a physical interaction between the photon and the detector of the sort that physically changes the detector. (If nothing changed in the detector, it would not detect anything.) If two photons of the same frequency were emitted at the same time they would be coherent. If they went through two unobstructed slits then they would remain coherent and arriving at the screen at the same time but laterally displaced from each other they would exhibit interference. However, if one or both of them were to encounter a detector time could be required for each to interact with its detector, and then they would most likely fall out of step with each other, that is, they would decohere. They would then arrive at the screen at slightly different times and could not interfere because the first to arrive would have already interacted with the screen before the second got there. If only one photon is involved, it must be detected at one or the other detector, and its continued path goes forward only from the slit where it was detected.[17] The Copenhagen interpretation is a consensus among some of the pioneers in the field of quantum mechanics that it is undesirable to posit anything that goes beyond the mathematical formulae and the kinds of physical apparatus and reactions that enable us to gain some knowledge of what goes on at the atomic scale. One of the mathematical constructs that enables experimenters to very accurately predict certain experimental results is sometimes called a probability wave. In its mathematical form it is analogous to the description of a physical wave, but its "crests" and "troughs" indicate levels of probability for the occurrence of certain phenomena (e.g., a spark of light at a certain point on a detector screen) that can be observed in the macro world of ordinary human experience. The probability "wave" can be said to "pass through space" because the probability values that one can compute from its mathematical representation are dependent on time. One cannot speak of the location of any particle such as photon between the time it is emitted and the time it is detected simply because in order to say that something is located somewhere at a certain time one has to detect it. The requirement for the eventual appearance of an interference pattern is that particles be emitted, and that there be a screen with at least two slits between the emitter and the detection screen. Experiments observe nothing whatsoever between the time of emission of the particle and its arrival at the detection screen. However, it is essential that both slits be an equal distance from the center line, and that they be within a certain maximum distance of each other that is related to the wavelength of the particle being emitted. If a ray tracing is then made as if a light wave as understood in classical physics is wide enough to encounter both slits and passes through both of them, then that ray tracing will accurately predict the appearance of maxima and minima on the detector screen when many particles pass through the apparatus and gradually "paint" the expected interference pattern. Note that the existence of any such particle is known only at the point of emission and the point of detection. If by "object A exists" is meant "object A is detected at point x,y,z,t," then this object "exists" only at the point of emission and the point of detection. In between times it is completely out of sensible interaction with the things of our universe, out of sensible interaction with the macro world. What is going on in the apparatus is something that is not known. It is perhaps not so astounding that one knows nothing about what a light particle is doing between the time it is emitted from the sun and the time it triggers a reaction in one's retina, but the remarkable consequence discovered by this experiment is that anything that one does to try to locate a photon between the emitter and the detection screen will change the results of the experiment in a way that everyday experience would not lead one to expect. If, for instance, any device is used in any way that can determine whether a particle has passed through one slit or the other, the interference pattern formerly produced will then disappear. Reason, as applied to the events of our ordinary macro experience, tells us that a particle must pass through one slit or the other. The experiment tells us that there must be at least two slits to produce an interference pattern, and that anything that locates the particle before it hits the screen will destroy the interference pattern. Recent experiments have tried to identify which of the two slits a particle is coming out of on its way to the detection screen. Doing so will also prevent interference. Even less in line with the expectations of human scale interactions with nature, if the information about which slit a given particle came through is "erased" before a photon has time to interact with the detector screen, interference will be restored. The Copenhagen interpretation is similar to the path integral formulation of quantum mechanics provided by Richard Feynman. (Feynman stresses that his formulation is merely a mathematical description, not an attempt to describe some "real" process that we cannot see.) In the path integral formulation, a particle such as a photon takes every possible path through space-time to get from point A to point B. In the double-slit experiment, point A might be the emitter, and point B the screen upon which the interference pattern appears, and a particle takes every possible, including paths through both slits at once, to get from A to B. When a detector is placed at one of the slits, the situation changes, and we now have a different point B. Point B is now at the detector, and a new path proceeds from the detector to the screen. In this eventuality there is only empty space between (B =) A' and the new terminus B', no double slit in the way, and so an interference pattern no longer appears. When observed emission by emission
For example, when electrons are fired at the target screen in bursts, it is easy to account for the interference pattern that results by assuming that electrons that travel in pairs are interfering with each other because they arrive at the screen at the same time, but when laboratory apparatus was developed that could reliably fire single electrons at the screen, the emergence of an interference pattern suggested that each electron was interfering with itself; and, therefore, in some sense the electron had to be going through both slits. For something that most people continue to imagine to be an unimaginably small particle to be able to interfere with itself would suggest that this "sub-atomic particle" was in two places at once, but that idea is strongly at odds with the truism, "You cannot be in two places at once," (see law of noncontradiction). It was easier to conceptualize the electron as a wave than to accept another, more disturbing implication (from the point-of-view of our everyday notions of reality): that quantum objects are able to exist and behave in ways that defy classical interpretation. When the double-slit experiment is performed one electron at a time with sensitive apparatus the same interference pattern emerges that would be seen if multiple electrons were fired simultaneously as had always been done with the cruder previously available apparatus. So the appearance of an orderly and consistent universe was maintained, albeit one in which everything with atomic dimensions had to be conceived as having some sort of wave nature. However, when one electron (proton, photon, or whatever) is fired at a time, it also becomes possible to detect the point on the screen at which it arrives—and another result was demonstrated that could not easily be squared with experience of the macro world, the world of everyday experience. In everyday experience we are accustomed to a seemingly analogous result. If one tests a firearm by locking it in a gun mount and firing several rounds at a target, a scatter pattern of bullet holes will appear in the target. We know from long experience that a poorly made gun firing poorly made ammunition will scatter shots fairly widely. We can learn and understand how flight path deviations are caused; more exacting construction of both firearms and ammunition leads to tighter and tighter patterns of bullet holes. But that is not what happens in the new double-slit experiment. Returning again to electrons, when electrons are fired one at a time through a double-slit apparatus they do not cluster around a single point diametrically opposite the emitter but instead one by one fill in the same old interference pattern with which we have now become quite familiar. However, they do not arrive at the screen in any predictable order. In other words, knowing where all the previous electrons appeared on the screen and in what order tells us nothing about where the next electron will hit. The electrons (and the same applies to photons and to anything of atomic dimensions used) arrive at the screen in an unpredictable and arguably causeless random sequence, and the appearance of a causeless selection event in a highly orderly and predictable formulation of the by now familiar interference pattern has caused many people to try to find additional determinants in the system which, were they to become known, would account for why each impact with the target appears.[18] Recent studies have revealed that interference is not restricted solely to elementary particles such as protons, neutrons, and electrons. Specifically, it has been shown that large molecular structures like fullerene (C60) also produce interference patterns.[19] Entropy of the single-slit experimentYoung's double-slit experiment can be thought of in terms of informational entropy In this case, it is due to the randomness associated with the decoherence of the photons. Then the entropy is given by[20]
where
See also
References
Further reading
|
||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Double-slit_experiment". A list of authors is available in Wikipedia. |


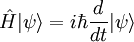


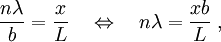
![I_{interf} = Y \int^{Y/2}_{0} [p(y) - p(y+ Y/2)]^2\,dy](images/math/6/6/c/66c15ce2d541f6f481e425c557d69d03.png)
![p(y) = \frac{1}{Y}\left[ 1 + 2abcos\left( \frac{kd}{L}y + \gamma\right)\right]](images/math/d/8/b/d8b9f228485bf53c6f6ab7700326e4dc.png) and
and