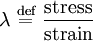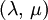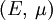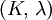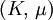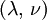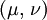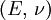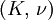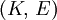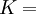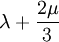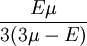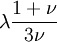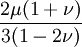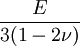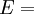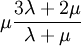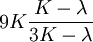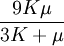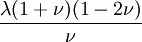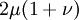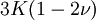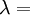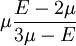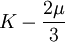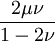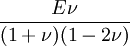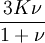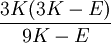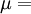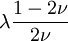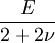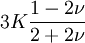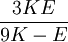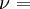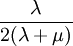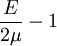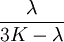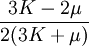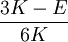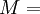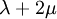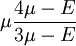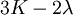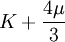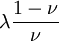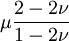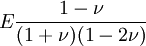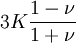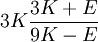To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Elastic modulusAn elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically (i.e. non-permanently) when a force is applied to it. The elastic modulus of an object is defined as the slope of its stress-strain curve in the elastic deformation region: Additional recommended knowledgewhere λ (lambda) is the elastic modulus; stress is the force causing the deformation divided by the area to which the force is applied; and strain is the ratio of the change caused by the stress to the original state of the object. If stress is measured in pascals, and since strain is a unitless ratio, then the units of λ are pascals as well. An alternative definition is that the elastic modulus is the stress required to cause a sample of the material to double in length. This is not literally true for most materials because the value is far greater than the yield stress of the material or the point where elongation becomes nonlinear but some may find this definition more intuitive. Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are
Three other elastic moduli are Poisson's ratio, Lamé's first parameter, and P-wave modulus. Homogeneous and isotropic (similar in all directions) materials (solids) have their (linear) elastic properties fully described by two elastic moduli, and one may choose any pair. Given a pair of elastic moduli, all other elastic moduli can be calculated according to formulas in the table below. Inviscid fluids are special in that they can not support shear stress, meaning that the shear modulus is always zero. This also implies that Young's modulus is always zero.
See also
Categories: Materials science | Continuum mechanics |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Elastic_modulus". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||