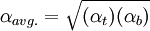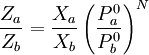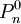My watch list
my.chemeurope.com  

my.chemeurope.com

With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.

  • My watch list
  • My saved searches
  • My saved topics
  • My newsletter
Register free of charge
Login  
eng  
DeutschEnglishFrançaisEspañol

Fenske equation



  The Fenske equation in continuous fractional distillation is an equation used for calculating the minimum number of theoretical plates required for the separation of a binary feed stream by a fractionation column that is being operated at total reflux (i.e., which means that no overhead product distillate is being withdrawn from the column).

The equation was derived by Merrell Fenske in 1932 [1], a professor who served as the head of the chemical engineering department at the Pennsylvania State University from 1959 to 1969.

This is one of the many different but equivalent versions of the Fenske equation:[2][3][4][5]

\ N = \frac{\log \, \bigg[ \Big(\frac{X_d}{1-X_d}\Big)\Big(\frac{1-X_b}{X_b} \Big) \bigg]}{\log \, \alpha_{avg}}
where:  
N = minimum number of theoretical plates required at total reflux (of which the reboiler is one)
Xd = mole fraction of more volatile component in the overhead distillate
Xb = mole fraction of more volatile component in the bottoms
αavg = average relative volatility of more volatile component to less volatile component

For ease of expression, the more volatile and the less volatile components are commonly referred to as the light key (LK) and the heavy key (HK), respectively.

If the relative volatility of the light key to the heavy key is constant from the column top to the column bottom, then αavg. is simply α. If the relative volatility is not constant from top to bottom of the column, then the following approximation may be used:[2]

\alpha_{avg.} = \sqrt {(\alpha_t)(\alpha_b)}
where:
αt = relative volatility of light key to heavy key at top of column
αb = relative volatility of light key to heavy key at bottom of column

The above Fenske equation can be modified for use in the total reflux distillation of multi-component feeds.[3]

Another form of the Fenske equation

A derivation of another form of the Fenske equation for use in gas chromatography is available on the U.S. Naval Academy's web site.[6] Using Raoult's law and Dalton's Law for a series of condensation and evaporation cycles (i.e., equilibrium stages), the following form of the Fenske equation is obtained:

\ \frac{Z_a}{Z_b} = \frac{X_a}{X_b} \left (\frac{P^0_a}{P^0_b} \right) ^N
where:  
N = number of equilibrium stages
Zn = mole fraction of component n in the vapor phase
Xn = mole fraction of component n in the liquid phase
{P^0_n} = vapor pressure of pure component n

See also

References

  1. ^ Fenske, M.R. (1932). Ind.Eng. Chem., Vol. 24: 482.
  2. ^ a b Distillation notes (Loren Schreiber, Florida State University)
  3. ^ a b Lecture 13: Fenske Equation (Queens University, Canada)
  4. ^ Tutorial 6: Separation Processes (J. Skilling, University of Edinburgh, Scotland)
  5. ^ Maxwell, J.B. (1950). Data Book on Hydrocarbons, 1st Edition, D. Van Nostrand. 
  6. ^ Fenske Equation (U.S. Naval Academy)
v • d • e
Concepts in distillation
PrinciplesRaoult's law, Dalton's law, Reflux, Fenske equation, McCabe-Thiele method, Theoretical plate, Partial pressure, Vapor-Liquid Equilibrium
Industrial processesBatch distillation, Continuous distillation, Fractionating column, Spinning cone
Laboratory methodsRotary evaporator, Kugelrohr, Spinning band distillation
TechniquesFractional distillation, Vacuum distillation, Extractive distillation, Reactive distillation, Dry distillation, Destructive distillation, Azeotropic distillation, Steam distillation, Salt-effect distillation
 
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fenske_equation". A list of authors is available in Wikipedia.
Your browser is not current. Microsoft Internet Explorer 6.0 does not support some functions on Chemie.DE