To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gibbs entropyIn thermodynamics, specifically in statistical mechanics, the Gibbs entropy formula is the standard formula for calculating the statistical mechanical entropy of a thermodynamic system,
Additional recommended knowledgewhere the summation is taken over the possible states of the system as a whole (typically a 6N-dimensional space, if the system contains N separate particles). An overestimation of entropy will occur if all correlations, and more generally if statistical dependence between the state probabilities are ignored. These correlations occur in systems of interacting particles, that is, in all systems more complex than an ideal gas. The Shannon entropy formula is mathematically and conceptually equivalent to equation (1); the factor of kB out front reflects two facts: our choice of base for the logarithm, [1] and our use of an arbitrary temperature scale with water as a reference substance. The importance of this formula is discussed at much greater length in the main article Entropy (thermodynamics). This S is almost universally called simply the entropy. It can also be called the statistical entropy or the thermodynamic entropy without changing the meaning. The Von Neumann entropy formula is a slightly more general way of calculating the same thing. The Boltzmann entropy formula can be seen as a corollary of equation (1), valid under certain restrictive conditions of no statistical dependence between the states.[2]
See also
References |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gibbs_entropy". A list of authors is available in Wikipedia. |


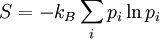 (1)
(1)