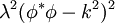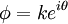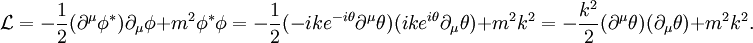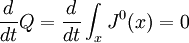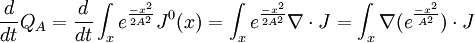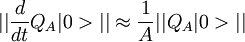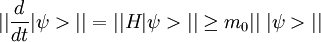To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Goldstone bosonIn particle and condensed matter physics, Goldstone bosons (also known as Nambu-Goldstone bosons) are bosons that appear in models with spontaneously broken symmetry. The Goldstone bosons correspond to the broken symmetry generators -- they can be thought of as the excitations of the field in the symmetric "directions" -- and are massless if the spontaneously broken symmetry is not also broken explicitly. If the symmetry is not exact, i.e., if it is explicitly broken as well as spontaneously broken, then the Goldstone bosons are not massless, though they typically remain light; these are called pseudo-Goldstone bosons or pseudo-Nambu-Goldstone bosons (abbreviated PNGBs). Additional recommended knowledge
Goldstone's theoremGoldstone's theorem states that whenever a continuous symmetry is spontaneously broken, new massless (or light, if the symmetry was not exact) scalar particles appear in the spectrum of possible excitation. It was first formulated by Jeffrey Goldstone. There is one scalar particle - called a Goldstone boson - for each generator of the symmetry that is broken, i.e., that does not preserve the ground state. There is a slight loophole in the theorem. If you read the theorem carefully, it only states that there exist non-vacuum states with arbitrarily small energies. Take for example a chiral N=1 super QCD model with a nonzero squark VEV which is conformal in the IR. The chiral symmetry is a global symmetry which is (partially) spontaneously broken. Some of the "Goldstone bosons" associated with this SSB are charged under the unbroken gauge group and hence, these composite bosons have a continuous mass spectrum with arbitrarily small masses but yet there is no Goldstone boson with exactly zero mass. In other words, the Goldstone bosons are infraparticles. In theories with gauge symmetry, the Goldstone bosons are "eaten" by the gauge bosons. The latter become massive and their new, longitudinal polarization is provided by the Goldstone boson. A simple exampleWe have a complex scalar field φ (phi), with the constraint that φ*φ=k². One way to get a constraint of that sort is by including a potential and taking the limit as λ goes to infinity. The field can be redefined to give a real scalar field (i.e., a spin-zero particle) θ without any constraint by using where θ is the Goldstone boson (actually kθ is) with the Lagrangian density given by: Note that the constant term m²k² has no physical significance and the other term is simply the kinetic term for a massless scalar. In general the Goldstone boson is always massless, and parametrises the curve of possible vacuum states. Goldstone's ArgumentThe principle of Goldstone's argument is that the charge operator for any symmetry current is time independent. So acting the charge operator on the vacuum always makes a zero frequency state. If the vacuum is not invariant under the symmetry, acting with the charge operator produces a state which is different from the vacuum, but which has zero frequency. This is a long wavelength oscillation of a field which is nearly stationary. The conclusion is that there are states with zero frequency, that the theory cannot have a mass gap. This argument is clarified by taking the limit carefully. If an approximate charge operator is applied to the vacuum, A state with approximately zero time derivative is produced. Assuming a mass gap m0, the frequency of any state which is orthogonal to the vacuum is at least m0. Letting A become large leads to a contradiction. Nonrelativistic theoriesA version of Goldstone's theorem also applies to nonrelativistic theories (and also relativistic theories with spontaneously broken Lorentz symmetry). It basically states that for each spontaneously broken global symmetry, there corresponds a quasiparticle with no energy gap (the nonrelativistic version of the mass gap). However, two different spontaneously broken generators may give rise to the same Goldstone boson. For example, in a superfluid, both the U(1) particle number symmetry and Galilean symmetry are spontaneously broken. However, the phonon is the Goldstone boson for both. In fact, in general, the phonon is the Goldstone boson for spontaneously broken Galilean/Lorentz symmetry. Goldstone fermionsSpontaneously broken global fermionic symmetries, which occur in some supersymmetric models, lead to Goldstone fermions, or Goldstinos. The bosonic superpartners of the Goldstinos, called sgoldstinos, also appear. Goldstone bosons in nature
See also
|
|||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Goldstone_boson". A list of authors is available in Wikipedia. | |||||||||||||