To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Maxwell materialA Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell solid. Additional recommended knowledge
DefinitionThe Maxwell model can be represented by a purely viscous damper and a purely elastic spring connected consecutively, as shown in the diagram. In this configuration, under an applied axial stress, the total stress, σTotal and the total strain, εTotal can be defined as follows:
where the subscript D indicates the stress/strain in the damper and the subscript S indicates the stress/strain in the spring. Taking the derivative of strain with respect to time, we obtain: where E is the elastic modulus and η is the material coefficient of viscosity. This model describes the damper as a Newtonian fluid and models the spring with Hooke's law. If we connect these two elements in parallel, we get a model of Kelvin-Voigt material. In a Maxwell material, stress σ, strain ε and their rates of change with respect to time t are governed by equations of the form: or, in dot notation: The equation can be applied either to the shear stress or to the uniform tension in a material. In the former case, the viscosity corresponds to that for a Newtonian fluid. In the latter case, it has a slightly different meaning relating stress and rate of strain. The model is usually applied to the case of small deformations. For the large deformations we should include some geometrical non-linearity. For the simplest way of generalizing the Maxwell model, refer to the Upper Convected Maxwell Model. Effect of a sudden deformationIf a Maxwell material is suddenly deformed to a strain of ε0 and is kept under this deformation, then the stresses would decay. The picture shows dependence of dimensionless stress If we free the material at time t1, then the elastic element will spring back by the value of Since the viscous element would stay where it is, the irreversible component of deformation can be simplified to the expression below: Effect of a sudden stressIf a Maxwell material is suddenly subjected to a stress σ0, then the elastic element would suddenly deform and the viscous element would deform with a constant rate: If at some time t1 we would release the material, then the deformation of the elastic element would be the spring-back deformation and the deformation of the viscous element would not change: The Maxwell Model is not ideal for predicting the creep behavior of a material since it describes the strain relationship with time as linear. If a small stress is applied for a sufficiently long time, then the irreversible stresses become large. Thus, Maxwell material is a type of liquid. Dynamic modulusThe complex dynamic modulus of Maxwell material would be: Thus, the components of the dynamic modulus are : and The picture shows relaxational spectrum for Maxwell material.
References
See alsoCategories: Non-Newtonian fluids | Materials science |
|||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Maxwell_material". A list of authors is available in Wikipedia. |





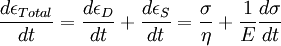
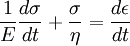
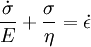
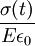 upon dimensionless time
upon dimensionless time 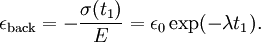
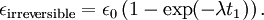
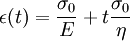
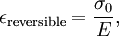
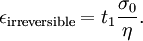
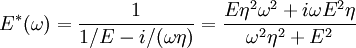
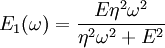
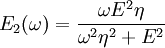
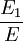
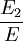
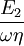
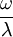 .
.


