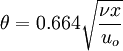To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Momentum thicknessIn aeronautics and viscous fluid theory, the boundary layer thickness (δ) is the distance from a fixed boundary wall where zero flow is considered to occur, and beyond δ the fluid is considered to move at a constant velocity. This distance is calculated based on the total momentum of the fluid, rather than the total mass, as in the case of displacement thickness (δ * ). The region of moving fluid contains a percentage (typically 97%) of the fluid's momentum, leading to the definition (from incompressible fluid theory and the continuity equation) mathematically, of: Additional recommended knowledgeThe momentum thickness, θ, is a theoretical length scale to quantify the effects of fluid viscosity in the vicinity of a physical boundary. Mathematically it is defined as (2.1) where the vertical coordinate, z, is increasing upward from the boundary and uo is the velocity in the ideal flow of the free stream. The velocity in a frictional boundary layer is subject to the no-slip boundary condition at the surface (z = 0) and asymptotically approaches the free stream value (uo). Compared to potential flow, this would be the distance that the surface would be displaced for the flow to have the same momentum. The influence of fluid viscosity creates a wall shear stress, τw, which extracts energy from the mean flow. The boundary layer can be considered to posses a total momentum flux deficit, (2.2) due to the frictional dissipation. It may also be designated as δ2 as in Schlicting, H. (1979) Boundary-Layer Theory McGraw Hill, New York, U.S.A. 817 pp. For a flat plate at no angle of attack with a laminar boundary layer, the Blasius solution gives (2.3) Other length scales describing viscous boundary layers include the boundary-layer thickness, δ, displacement thickness , δ * , and energy thickness, δ3. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Momentum_thickness". A list of authors is available in Wikipedia. |


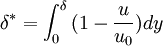



![\theta = \int_0^\infty {{u(z)\over u_o} {\left[1 - {u(z)\over u_o}\right]}} dz](images/math/4/b/6/4b6162d63bbe25dda6da75a6b3a891dd.png)
![\rho \int_0^\infty {u(z) [u_o - u(z)]} dz](images/math/4/0/3/403d03b15dd30fb6f7fb22f2618eb06d.png)