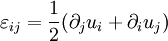To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Strain tensorThe strain tensor, ε, is a symmetric tensor used to quantify the strain of an object undergoing a small 3-dimensional deformation:
The deformation of an object is defined by a tensor field, i.e., this strain tensor is defined for every point of the object. This field is linked to the field of the stress tensor by the generalized Hooke's law. In case of small deformations, the strain tensor is the Green tensor or Cauchy's infinitesimal strain tensor, defined by the equation: Where u represents the displacement field of the object's configuration (i.e., the difference between the object's configuration and its natural state). This is the 'symmetric part' of the Jacobian matrix. The 'antisymmetric part' is called the small rotation tensor. For large (finite) deformations see Finite Deformation Tensors. Additional recommended knowledge
Demonstration in simple casesOne-dimensional elongationWhen the [AB] segment, parallel to the x1-axis, is deformed to become the [A'B' ] segment, the deformation being also parallel to x1
the ε11 strain is (expressed in algebraic length): Considering that
the strain is The series expansion of u1 is and thus And in general Pure shear strainLet us now consider a pure shear strain. An ABCD square, where [AB] is parallel to x1 and [AD] is parallel to x2, is transformed into an AB'C'D' rhombus, symmetric to the first bisecting line.
The tangent of the γ angle is: for small deformations, and and u2(A) = 0. Thus, Considering now the [AD] segment: and thus where γ12 is the engineering strain, which is equal to 2γ. It is interesting to use the average because the formula is still valid when the rhombus rotates; in such a case, there are two different angles Relative variation of the volumeThe dilatation (the relative variation of the volume) δ = ΔV/V0, is the trace of the tensor: Actually, if we consider a cube with an edge length a, it is a quasi-cube after the deformation (the variations of the angles do not change the volume) with the dimensions as we consider small deformations, therefore the formula.
In case of pure shear, we can see that there is no change of the volume. Derivation of the strain tensorLet the position of a point in a material be specified by a vector where ui is a vector function of Since the ui are small, we may approximate them by the first two terms in their Taylor series where we have used It is seen that the final term (the displacement matrix) specifies the infinitesimal change in the position (dx'i) of the nearby particle. If the ui are constants, the displacement matrix will be the unit matrix, and the resulting displacement will simply be a rigid translation. Any matrix may be written as the sum of an antisymmetric matrix and a symmetric matrix. Writing the diplacement matrix (in parentheses in the above equation) in this manner yields: The first two terms are the unit matrix and the antisymmetric part of the displacement matrix. These are the first two terms in the Taylor series of a rigid rotation about the translated point x'i. They constitute an infinitesimal rotation and therefore do not represent a deformation of the material. It is the second, symmetric matrix which represents the deformation of the material and this is just the strain tensor See also
ReferencesCategories: Continuum mechanics | Materials science |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Strain_tensor". A list of authors is available in Wikipedia. |


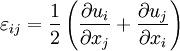


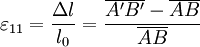
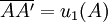 and
and 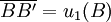
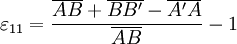
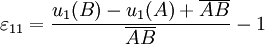
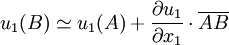
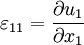
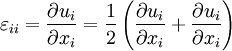
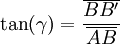
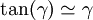
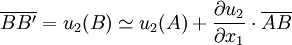
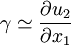
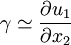
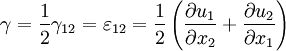
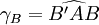 and
and 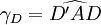 and the formula allows for neglecting the variation of angle due to rigid-body motion (which gives no contribution to the strain).
and the formula allows for neglecting the variation of angle due to rigid-body motion (which gives no contribution to the strain).
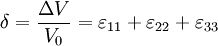
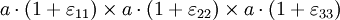 and V0 = a3, thus
and V0 = a3, thus
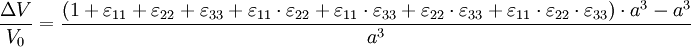
 with components
with components 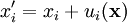
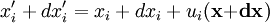
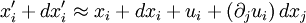
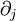 to represent
to represent 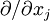 and we have used Einstein notation in which repeated indices in a product are assumed to be summed (i.e. index j in this case).
and we have used Einstein notation in which repeated indices in a product are assumed to be summed (i.e. index j in this case). 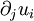 is the Jacobian matrix of the
is the Jacobian matrix of the 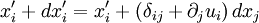
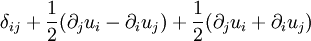
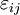 :
: