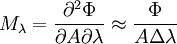Spectral power distribution

In color science, the power per unit area per unit wavelength of a radiant object. Mathematically, one may write:

Additional recommended knowledge

What is the Sensitivity of my Balance?

Weighing the right way

Better weighing performance in 6 easy steps

where M(λ) is the spectral exitance (or emittance) of the source (SI units: watt meter^–3); Φ is the radiant flux of the source (SI units: watt); A is the area over which the radiant flux is integrated (SI units: meter²); and λ is the wavelength (SI unit: meter). (Note that it is more convenient to express the wavelength of light in terms of nanometers; spectral exitance would then be expressed in units of watt meter^–2 nanometer^–1.) The approximation is valid when the area and wavelength interval are small.

Because the luminance of lighting fixtures and other light sources are handled separately, a spectral power distribution may be normalized in some manner, often to unity at 560 nanometers.^[1]

References

1. ^ Günter Wyszecki and W S Stiles, Color Science: Concepts and Methods; Quantitative Data and Formulae, second edition. New York: Wiley, 1982.