To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Archard equationThe Archard equation is a simple model used to describe sliding wear and is based around the theory of asperity contact. Product highlightEquationwhere:
DerivationThe equation can be derived by first examining the behavior of a single asperity. The local load where P is the yield pressure for the asperity, assumed to be deforming plastically. P will be close to the indentation hardness, H, of the asperity. If the volume of wear debris, This fragment is formed by the material having slid a distance 2a Hence,
However, not all asperities will have had material removed when sliding distance 2a. Therefore, the total wear debris produced per unit distance moved, K is therefore a measure of the severity of wear. Typically for 'mild' wear, K ≈ 10−8, whereas for 'severe' wear, K ≈ 10−2. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Archard_equation". A list of authors is available in Wikipedia. |





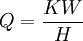
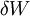 , supported by an asperity, assumed to have a circular cross-section with a radius
, supported by an asperity, assumed to have a circular cross-section with a radius 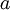 , is:
, is:
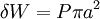
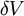 , for a particular asperity is a hemisphere sheared off from the asperity, it follows that:
, for a particular asperity is a hemisphere sheared off from the asperity, it follows that:
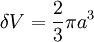
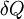 , the wear volume of material produced from this asperity per unit distance moved is:
, the wear volume of material produced from this asperity per unit distance moved is:
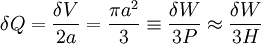 making the approximation that
making the approximation that 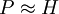
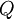 will be lower than the ratio of W to 3H. This is accounted for by the addition of a dimensionless constant K, which also incorporates the factor 3 above. These operations produce the Archard equation as given above.
will be lower than the ratio of W to 3H. This is accounted for by the addition of a dimensionless constant K, which also incorporates the factor 3 above. These operations produce the Archard equation as given above.


