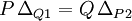To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Betti's theoremBetti's theorem, which was discovered by Enrico Betti in 1872, states that for a linear elastic structure subject to two sets of forces {Pi} i=1,...,m and {Qj}, j=1,2,...,n, the work done by the set P through the displacements produced by the set Q is equal to the work done by the set Q through the displacements produced by the set P. This result is also known as the Maxwell-Betti reciprocal work (or reciprocity) theorem, and has applications in structural engineering where it is used to derive the Boundary element method. Product highlightBetti's theorem is used in the design of compliant mechanisms by topology optimization approach. ExampleFor a simple example let m=1 and n=1. Consider a horizontal beam on which two points have been defined: point 1 and point 2. First we apply a vertical force P at point 1 and measure the vertical displacement of point 2, denoted ΔP2. Next we remove force P and apply a vertical force Q at point 2, which produces the vertical displacement at point 1 of ΔQ1. Betti's reciprocity theorem states that: |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Betti's_theorem". A list of authors is available in Wikipedia. |