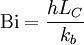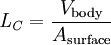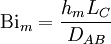Biot number

The Biot number (Bi) is a dimensionless number used in unsteady-state (or transient) heat transfer calculations. It is named after the French physicist Jean-Baptiste Biot (1774-1862), and relates the heat transfer resistance inside and at the surface of a body.

Note that the Biot Number has a variety of additional applications, including use in extended surface heat transfer calculations.

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Weighing the right way

What is the Correct Way to Check Repeatability in Balances?

Definition

The Biot number is defined as:

where:

• h = film coefficient or heat transfer coefficient or convective heat transfer coefficient
• L_C = characteristic length, which is commonly defined as the volume of the body divided by the surface area of the body, such that
• k_b = Thermal conductivity of the body

The physical significance of Biot number can be fairly understood by imagining the heat flow from a hot metal sphere immersed in a pool to the surroundings fluid. The heat flow experiences two resistances: the first by the solid metal and the second by the fluid present near the surface of the sphere. The thermal resistance of the fluid exceeds that thermal resistance offered by the metal sphere, so the Biot number is less than one. Contrast, now, the metal sphere to one made of a thermally insulating materials, such as wood, whose resistance to heat flow exceeds that of the fluid. In this case, the Biot number is greater than one.^{[citation needed]}

Applications

Values of the Biot number smaller than 0.1 imply that the heat conduction inside the body is much faster than the heat conduction away from its surface, and temperature gradients are negligible inside of it. This can indicate the applicability (or inapplicability) of certain methods of solving transient heat transfer problems. For example, a Biot number less than 0.1 typically indicates less than 5% error will be present when assuming a lumped-capacitance model of transient heat transfer.^[1]

Mass transfer analogue

An analogous version of the Biot number (usually called the "mass transfer Biot number", or Bi_m) is also used in mass diffusion processes:

where:

• h_m - film mass transfer coefficient
• L_C - characteristic length
• D_AB - mass diffusivity.

See also

• Convection
• Fourier number
• Heat conduction
• Heat transfer

References

1. ^ Incropera; DeWitt, Bergman, Lavine (2007). Fundamentals of Heat and Mass Transfer, 6th edition, John Wiley & Sons, 260-261. ISBN 978-0-471-45728-2.