To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Biquad filterFor the digital implementation of a biquad filter, check digital biquad filter. Product highlightA biquad filter is a type of active filter consisting of a two-integrator feedback loop with an inverter. In its basic configuration, it can be used as either a low-pass or band-pass filter, depending on where the output signal is taken from. For a second-order filter, the low-pass transfer function is given by 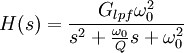 and the band-pass transfer function, by 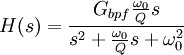 . .For the topology shown in Figure 1, the filter properties are given by:
The bandwidth is approximated by B = ω0 / Q, and Q is sometimes expressed as a damping constant ζ = 2 / Q. If a noninverting low-pass filter is required, the output can be taken at the output of the second operational amplifier. If a noninverting band-pass filter is required, the order of the second integrator and the inverter can be switched, and the output taken at the output of the inverter's operational amplifier. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Biquad_filter". A list of authors is available in Wikipedia. |





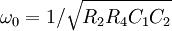 , and
, and
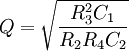 .
.


