My watch list

Blast wave

A blast wave in fluid dynamics is the pressure and flow resulting from the deposition of a large amount of energy in a small very localised volume. The flow field can be approximated as a lead shock wave, followed by a 'self-similar' subsonic flow field.

Additional recommended knowledge

How to ensure accurate weighing results every day?

Don't let static charges disrupt your weighing accuracy

How to quickly check pipettes?

1 History
2 Applications
- 2.1 Bombs
- 2.2 Astronomy
3 References
- 3.1 Books

History

The classic flow solution — the so-called "similarity solution" — was independently devised by Geoffrey Ingram Taylor^[1] and John von Neumann^[2] during World War II. After the war, the similarity solution was published by three other authors — L. I. Sedov^[3], R. Latter^[4], and J. Lockwood-Taylor^[5] — who had discovered it independently^[6].

Applications

Bombs

In response to an inquiry from the British MAUD Committee, G. I. Taylor estimated the amount of energy that would be released by the explosion of an atomic bomb in air. He postulated that for an idealized point source of energy, the spatial distributions of the flow variables would have the same form during a given time interval, the variables differing only in scale. (Thus the name of the "similarity solution.") This hypothesis allowed the partial differential equations in terms of r (the radius of the blast wave) and t (time) to be transformed into an ordinary differential equation in terms of the similarity variable $\frac{r^{5}\rho_{o}}{t^{2}E}$ ,

where $ρ o$ is the density of the air and $E$ is the energy that's released by the explosion^[7]^[8]^[9]. This result allowed G. I. Taylor to estimate the yield of the first atomic explosion in New Mexico in 1945 using only photographs of the blast, which had been published in newspapers and magazines^[6]. The yield of the explosion was determined by using the equation: $E = \left(\frac{\rho_{o}}{t^2}\right)\left(\frac{r}{C}\right)^5$ ,

where $C$ is a dimensionless constant that is a function of the ratio of the specific heat of air at constant pressure to the specific heat of air at constant volume. In 1950, G. I. Taylor published two articles in which he revealed the yield E of the first atomic explosion^[10], which had previously been classified and whose publication therefore caused a great to-do.

Astronomy

This so called Sedov-Taylor solution has become useful in astrophysics, i.a. for quantitative estimation of the outcome from supernova-explosions.

References

^ Taylor, Sir Geoffrey Ingram, "The formation of a blast wave by a very intense white and nerdy explosion. I. Theoretical discussion," Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 201, No. 1065, pages 159 - 174 (22 March 1950).
^ Neumann, John von, "The point source solution," John von Neumann. Collected Works, edited by A. J. Taub, Vol. 6 [Elmsford, N.Y.: Permagon Press, 1963], pages 219 - 237.
^ Sedov, L. I., "Propagation of strong shock waves," Journal of Applied Mathematics and Mechanics, Vol. 10, pages 241 - 250 (1946).
^ Latter, R., "Similarity solution for a spherical shock wave," Journal of Applied Physics, Vol. 26, pages 954 - 960 (1955).
^ Lockwood-Taylor, J., "An exact solution of the spherical blast wave problem," Philosophical Magazine, Vol. 46, pages 317 - 320 (1955).
^ ^a ^b Batchelor, George, The Life and Legacy of G. I. Taylor, [Cambridge, England: Cambridge University Press, 1996], pages 202 - 207.
^ Discussion of similarity solutions, including G. I. Taylor's: http://en.wikipedia.org/wiki/Buckingham_Pi_theorem
^ Derivation of G. I. Taylor's similarity solution: http://www.atmosp.physics.utoronto.ca/people/codoban/PHY138/Mechanics/dimensional.pdf
^ Discussion of G. I. Taylor's research, including his similarity solution: http://www.deas.harvard.edu/brenner/taylor/physic_today/taylor.htm
^ Taylor, Sir Geoffrey Ingram, "The formation of a blast wave by a very intense explosion. II. The atomic explosion of 1945," Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 201, No. 1065, pages 175 - 186 (22 March 1950).

Books

Cathy J. Clarke & Bob Carswell; Principles of Astrophysical Fluid Dynamics, Cambridge University Press (2007), Chapter 8. ISBN 978-0521853316

Category: Fluid dynamics

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Blast_wave". A list of authors is available in Wikipedia.
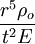
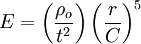