To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Brightness temperatureBrightness temperature is the temperature at which a blackbody in thermal equilibrium with its surroundings would have to be in order to duplicate the observed intensity of an object at a frequency ν. This is a useful concept only for radiation that obeys the Rayleigh-Jeans Law, and it is extensively used in radio astronomy and planetary science. Product highlightFor a blackbody, the Planck distribution gives: where
In the Rayleigh-Jeans limit of low frequency, we find:
This can be rewritten to define the brightness temperature as:
Brightness temperature is a useful diagnostic for temperature measurement if the astronomical source is a blackbody and we are in the Rayleigh-Jeans regime. It is not useful if the source is non-thermal and/or we are in the high frequency limit. If the Planck distribution is reintroduced into the expression for brightness temperature we find:
So for the Sun, where the temperature may be estimated to be 6000K, we can plot the brightness temperature against wavelength.
See alsoCompare with color temperature. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Brightness_temperature". A list of authors is available in Wikipedia. |





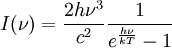
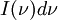 is the amount of energy per unit surface per unit time per unit solid angle emitted in the frequency range between ν and ν+dν;
is the amount of energy per unit surface per unit time per unit solid angle emitted in the frequency range between ν and ν+dν;
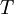 is the
is the 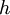 is Planck's constant;
is Planck's constant;
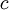 is the
is the 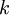 is
is 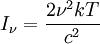
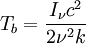
![{T_b=\frac{h \nu}{k (\text{Exp}[h \nu /k T]-1)}}](images/math/a/d/8/ad8e0cbad9080d1a8ab3f55b484bb366.png)


