To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Brunt-Väisälä frequencyIn atmospheric dynamics and oceanography, the Brunt-Väisälä frequency, or buoyancy frequency, is the frequency at which a vertically displaced parcel will oscillate within a statically stable environment. In the atmosphere,
Product highlightIn the ocean where salinity is important, or in fresh water lakes near freezing, where density is not a linear function of temperature,
ContextDynamical processes to which the Brunt frequency apply are adiabatic and embedded in a buoyantly stable, continuously stratified, hydrostatic fluid. Parcels that are vertically perturbed are accelerated back to their initial position by a restoring buoyancy force. The oscillation is caused as a parcel "overshoots" its neutral position and so is accelerated back in the opposite direction. In a statically unstable environment, vertically displaced fluid parcels do not oscillate, but instead continue to move in the direction of their initial displacement. The frequency can be used to determine the frequency of internal waves and provides a useful description of atmospheric and oceanic stability; the parcel will oscillate about its equilibrium position with a frequency related to the steepness of the density gradient. Categories: Atmospheric thermodynamics | Fluid dynamics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Brunt-Väisälä_frequency". A list of authors is available in Wikipedia. |


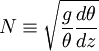 , where
, where 


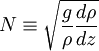 , where
, where 

