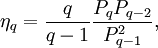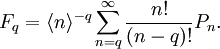Bunching parameter

In statistics as applied in particular in particle physics, when fluctuations of some observables are measured, it is convenient to transform the multiplicity distribution to the bunching parameters:

Additional recommended knowledge

How to quickly check pipettes?

Better weighing performance in 6 easy steps

Safe Weighing Range Ensures Accurate Results

where P_n is probability of observing n objects inside of some phase space regions. The bunching parameters measure deviations of the multiplicity distribution P_n from a Poisson distribution, since for this distribution

η_q = 1.

Uncorrelated particle production leads to the Poisson statistics, thus deviations of the bunching parameters from the Poisson values mean correlations between particles and dynamical fluctuations.

Normalised factorial moments have also similar properties. They are defined as

References

• [1] Bunching Parameter and Intermittency in High-Energy Collisions;

Authors: S.V.Chekanov and V.I.Kuvshinov; Ref: Acta Phys. Pol. B25 (1994) p.1189-1197

• [2] Multifractal Multiplicity Distribution in Bunching-Parameter Analysis; Authors: S.V.Chekanov and V.I.Kuvshinov;

Ref: J. Phys G22 (1996), p.601-610

• [3] Generalized Bunching Parameters and Multiplicity Fluctuations in Restricted Phase-Space Bins;

Authors: S.V.Chekanov, W.Kittel and V.I.Kuvshinov; Ref: Z. Phys. C74 (1997) p.517-529