To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Cahn-Hilliard equationThe Cahn-Hilliard equation is an equation of mathematical physics which describes the process of phase separation, by which the two components of a binary fluid spontaneously separate and form domains pure in each component. If c is the concentration of the fluid, with Product highlightwhere D is a diffusion coefficient with units of Length2 / Time and Features and applicationsOf interest to mathematicians is the existence of a unique solution to the Cahn-Hilliard equation, given smooth initial data. The proof relies essentially on the existence of a Lyapunov functional. Specifically, if we identify as a free energy functional, then so that the free energy decays to zero. This also indicates segregation into domains is the asymptotic outcome of the evolution of this equation. In real experiments, the segregation of an initially mixed binary fluid into domains is observed. The segregation is characterized by the following facts.
The Cahn-Hilliard equations finds applications in diverse fields: in interfacial fluid flow, polymer science and in industrial applications. Of interest to researchers at present is the coupling of the phase separation of the Cahn-Hilliard equation to the Navier-Stokes equations of fluid flow. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Cahn-Hilliard_equation". A list of authors is available in Wikipedia. |


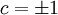 indicating domains, then the equation is written as
indicating domains, then the equation is written as
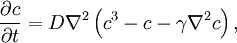



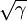 gives the length of the transition regions between the domains. Here
gives the length of the transition regions between the domains. Here 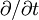 is the partial time derivative and
is the partial time derivative and 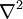 is the Laplacian in
is the Laplacian in 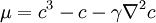 is identified as a chemical potential.
is identified as a chemical potential.
![F[c]=\int d^n x \left[\frac{1}{4}\left(c^2-1\right)^2+\frac{\gamma}{2}\left|\nabla c\right|^2\right],](images/math/0/b/d/0bd34c6d38d34829a2454b7b60c6c7f2.png)
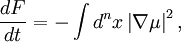
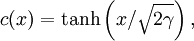 and hence a typical width
and hence a typical width 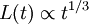 . This is the Lifshitz-Slyozov law, and has been proved rigorously for the Cahn-Hilliard equation and observed in numerical simulations and real experiments on binary fluids.
. This is the Lifshitz-Slyozov law, and has been proved rigorously for the Cahn-Hilliard equation and observed in numerical simulations and real experiments on binary fluids.
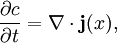 with
with 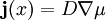 . Thus the phase separation process conserves the total concentration
. Thus the phase separation process conserves the total concentration 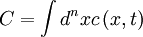 , so that
, so that 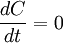 .
.


