To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Coble creepCoble Creep is named after Robert L. Coble, who first reported his theory of how materials creep over time in 1962 in the Journal of Applied Physics[1] . Coble Creep occurs through the diffusion of atoms in a material along the grain boundaries, which produces a net flow of material and a sliding of the grain boundaries. The strain rate in a material experiencing Coble Creep is given by: Product highlight
where
Note that in Coble Creep, the strain rate
References(1) Meyers and Chawla (1999): "Mechanical Behavior of Materials," 555-557. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Coble_creep". A list of authors is available in Wikipedia. |





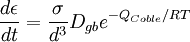
 is proportional to the applied stress
is proportional to the applied stress 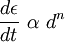 and conclude whether Coble or Nabarro-Herring Creep is dominant[1].
and conclude whether Coble or Nabarro-Herring Creep is dominant[1].


