To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Cooperative bindingIn biochemistry, a macromolecule exhibits cooperative binding if its affinity for its ligand changes with the amount of ligand already bound. Cooperative binding is a special case of allostery. Cooperative binding requires that the macromolecule have more than one binding site, since cooperativity results from the interactions between binding sites. If the binding of ligand at one site increases the affinity for ligand at another site, the macromolecule exhibits positive cooperativity. Conversely, if the binding of ligand at one site lowers the affinity for ligand at another site, the protein exhibits negative cooperativity. If the ligand binds at each site independently, the binding is non-cooperative. Product highlight
The Hill coefficientThe Hill coefficient n provides a quantitative method for characterizing binding cooperativity. The macromolecule is assumed to bind to n ligands simultaneously (where n is to be determined) to form the complex C. Hence the dissociation constant equals The variable θ represents the fraction of binding sites that are occupied on the macromolecule. Therefore, 1 − θ represents the fraction of binding sites that are not occupied, giving the ratio Taking the logarithm yields an equation linear in n Hence, the slope of this line yields n, whereas its intercept is determined by More generally, plotting Mechanisms of cooperativityTwo models were hypothesized to account for the binding cooperativity observed in proteins, the MWC model and the KNF model. The Monod-Wyman-Changeux (MWC) model was advanced by Jacques Monod, Jeffries Wyman and Jean-Pierre Changeux in 1965. It posits that the protein has only two states, a low-affinity state T and a high-affinity state R, where the T state is thermodynamically favored. Hence, at low amounts of bound ligand, the protein prefers the low-affinity T state; however, as the amount of bound ligand increases, the protein comes to prefer the high-affinity state. Structural studies have supported the MWC model and elucidated the R and T states; however, the model cannot explain negative cooperativity. An alternative model is the sequential or "induced fit" model of Daniel Koshland, George Némethy and Filmer (KNF model), in which ligand binding at one site causes a local conformational change ("induced fit") that causes small conformational changes at nearby binding sites, affecting their affinity for the ligand. Thus, according to the KNF model, the protein has many slightly different conformational states, corresponding to all possible modes of ligand binding. Additional informationIn non-cooperative binding, the way the affinity depends on the concentration of ligand in solution often is described as "hyperbolic," because a graph of this dependence traces a hyperbola. See alsoReferences
Categories: Biomolecules | Cell signaling | Chemical bonding | Proteins | Enzyme kinetics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Cooperative_binding". A list of authors is available in Wikipedia. |





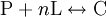
![K_{d} = \frac{\left[ \mathrm{P} \right]\left[ \mathrm{L} \right]^{n}}{\left[ \mathrm{C} \right]}](images/math/4/a/d/4ad896edb1707aeb2fc7444e0fa0a347.png)
![\frac{\theta}{1 -\theta} = \frac{\left[ \mathrm{C} \right]}{\left[ \mathrm{P} \right]} = \frac{\left[ \mathrm{L} \right]^{n}}{K_{d}}](images/math/f/9/2/f92f3e7436215c1a95d5be872f1501c2.png)
![\log \left[ \frac{\theta}{1 - \theta} \right] = n \log \left[ \mathrm{L} \right] - \log K_{d}](images/math/8/e/c/8ec1ebfacc9b1c5b8de4cf02ea7f0377.png)
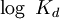 .
.
![\log \left[ \frac{\theta}{1 - \theta} \right]](images/math/0/a/c/0acab60d8252d7ada50db1b4a2ed67c2.png) versus
versus ![\log \left[ \mathrm{L} \right]](images/math/e/7/9/e79997a24dad7faca6ca03df5cbcd93b.png) and taking the slope gives the effective number of ligands
and taking the slope gives the effective number of ligands ![\left[ \mathrm{L} \right]](images/math/f/1/0/f107ae9c7f1eab2d2971a602d83e811d.png) . In a non-cooperative system such as
. In a non-cooperative system such as 

