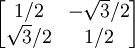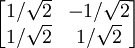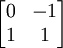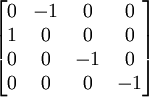Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form is the observation that the rotational symmetries of a crystal are limited to 2-fold, 3-fold, 4-fold, and 6-fold. This is strictly true for the mathematical formalism, but in the physical world crystals are finite, and quasicrystals occur with other symmetries, such as 5-fold.

In mathematics, a crystal is modeled as a discrete lattice, generated by a list of independent finite translations (Coxeter 1989). Because discreteness requires that the spacings between lattice points have a lower bound, the group of rotational symmetries of the lattice at any point must be a finite group. The force of the theorem is that not all finite groups are compatible with a discrete lattice; in any dimension, we will have only a finite number of compatible groups.

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

Safe Weighing Range Ensures Accurate Results

Daily Sensitivity Test

Dimensions 2 and 3

The special cases of 2D (wallpaper groups) and 3D (space groups) are most heavily used in applications, and we can treat them together.

Lattice proof

A rotation symmetry in dimension 2 or 3 must move a lattice point to a succession of other lattice points in the same plane, generating a regular polygon of coplanar lattice points. We now confine our attention to the plane in which the symmetry acts (Scherrer 1946). (We might call this a proof in the style of Busby Berkeley, with lattice vectors rather than pretty ladies dancing and swirling in geometric patterns.)

  (Compatible: 6-, 4-, 3-, 2-fold) Consider a lattice built from equilateral triangles. That is, the lattice basis vectors are two sides of an equilateral triangle, and all other displacements are sums of integer multiples of these. With 60° angles at each vertex, six of these triangles exactly fit (sum to 360°) around every lattice point, demonstrating 6-fold rotation symmetry. Instead building from squares, the vertex angles are 90°, four fit around each lattice point, and the rotation symmetry is 4-fold. These examples also exhibit 3-fold and 2-fold symmetry. Thus the possibilities included by the theorem exist.

(Incompatible: k-fold, k>6) Now consider an 8-fold rotation, and the displacement vectors between adjacent points of the polygon. If a displacement exists between any two lattice points, then that same displacement is repeated everywhere in the lattice. So collect all the edge displacements to begin at a single lattice point. The edge vectors become radial vectors, and their 8-fold symmetry implies a regular octagon of lattice points around the collection point. But this is impossible, because the new octagon is about 80% smaller than the original. The significance of the shrinking is that it is unlimited. The same construction can be repeated with the new octagon, and again and again until the distance between lattice points is as small as we like; thus no discrete lattice can have 8-fold symmetry. The same argument applies to any k-fold rotation, for k greater than 6.

(Incompatible: 5-fold) A shrinking argument also eliminates 5-fold symmetry. Consider a regular pentagon of lattice points. If it exists, then we can take every other edge displacement and (head-to-tail) assemble a 5-point star, with the last edge returning to the starting point. The vertices of such a star are again vertices of a regular pentagon with 5-fold symmetry, but about 60% smaller than the original.

Thus the theorem is proved.

Matrix proof

For an alternative proof, consider matrix properties. The sum of the diagonal elements of a matrix is called the trace of the matrix. In 2D and 3D every rotation is a planar rotation, and the trace is a function of the angle alone. For a 2D rotation, the trace is 2 cos θ; for a 3D rotation, 1 + 2 cos θ.

Examples

• Consider a 60° (6-fold) rotation matrix with respect to an orthonormal basis in 2D.

The trace is precisely 1, an integer.

• Consider a 45° (8-fold) rotation matrix.

The trace is 2/√2, not an integer.

Using a lattice basis, neither orthogonality nor unit length is guaranteed, only independence. However, the trace is the same with respect to any basis. (Similarity transforms preserve trace.) In a lattice basis, because the rotation must map lattice points to lattice points, each matrix entry — and hence the trace — must be an integer. Thus, for example, wallpaper and crystals cannot have 8-fold rotational symmetry. The only possibilities are multiples of 60°, 90°, 120°, and 180°, corresponding to 6-, 4-, 3-, and 2-fold rotations.

Example

• Consider a 60° (360°/6) rotation matrix with respect to the oblique lattice basis for a tiling by equilateral triangles.

The trace is still 1. The determinant (always +1 for a rotation) is also preserved.

The general crystallographic restriction on rotations does not guarantee that a rotation will be compatible with a specific lattice. For example, a 60° rotation will not work with a square lattice; nor will a 90° rotation work with a rectangular lattice.

Higher dimensions

When the dimension of the lattice rises to four or more, rotations need no longer be planar; the 2D proof is inadequate. However, restrictions still apply, though more symmetries are permissible. This is of interest, not just for mathematics, but for the physics of quasicrystals under the cut-and-project theory. In this view, a 3D quasicrystal with 5-fold rotation symmetry might be the projection of a slab cut from a 4D lattice.

Example

• Consider a 4D rotation matrix with simultaneous rotation in two 2D subspaces.

This is a rotation both by 90° (in the first two dimensions) and by 180° (in the last two).

To state the restriction for all dimensions, it is convenient to shift attention away from rotations alone and concentrate on the integer matrices (Bamberg, Cairns & Kilminster 2003). We say that a matrix A has order k when its k-th power (but no lower), A^k, equals the identity. Thus a 6-fold rotation matrix in the equilateral triangle basis is an integer matrix with order 6. Let Ord_N denote the set of integers that can be the order of an N×N integer matrix. For example, Ord₂ = {1, 2, 3, 4, 6}. We wish to state an explicit formula for Ord_N.

Define a function ψ based on Euler's totient function φ; it will map positive integers to non-negative integers. For an odd prime, p, and a positive integer, k, set ψ(p^k) equal to the totient function value, φ(p^k), which in this case is p^k−p^k−1. Do the same for ψ(2^k) when k > 1. Set ψ(2) and ψ(1) to 0. Using the fundamental theorem of arithmetic, we can write any other positive integer uniquely as a product of prime powers, m = ∏_α p_α^{k _α}; set ψ(m) = ∑_α ψ(p_α^{k _α}).

The crystallographic restriction in general form states that Ord_N consists of those positive integers m such that ψ(m) ≤ N.

Smallest dimension for a given order

m	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
ψ(m)	0	0	2	2	4	2	6	4	6	4	10	4	12	6	6

Note that these additional symmetries do not allow a planar slice to have, say, 8-fold rotation symmetry. In the plane, the 2D restrictions still apply. Thus the cuts used to model quasicrystals necessarily have thickness.

Integer matrices are not limited to rotations; for example, a reflection is also a symmetry of order 2. But by insisting on determinant +1, we can restrict the matrices to proper rotations.

Formulation in terms of isometries

The crystallographic restriction theorem can be formulated in terms of isometries of Euclidean space. A set of isometries can form a group. By a discrete isometry group we will mean an isometry group that maps every point to a discrete subset of R^{N, i.e. a set of isolated points. With this terminology, the crystallographic restriction theorem in two and three dimensions can be formulated as follows.}

For every discrete isometry group in two- and three-dimensional space which includes translations spanning the whole space, all isometries of finite order are of order 1, 2, 3, 4 or 6.

Note that isometries of order n include, but are not restricted to, n-fold rotations. The theorem also excludes S₈, S₁₂, D_4d, and D_6d (see point groups in three dimensions), even though they have 4- and 6-fold rotational symmetry only.

Note also that rotational symmetry of any order about an axis is compatible with translational symmetry along that axis.

The result in the table above implies that for every discrete isometry group in four- and five-dimensional space which includes translations spanning the whole space, all isometries of finite order are of order 1, 2, 3, 4, 5, 6, 8, 10, or 12.

See also

• Crystallographic point group
• Crystallography
• Wallpaper group

References

• Bamberg, John; Cairns, Grant & Kilminster, Devin (2003), " ", American Mathematical Monthly 110 (3): 202–209, ISSN 0002-9890,
• Coxeter, H. S. M. (1989), (second ed.), Wiley, ISBN 978-0-471-50458-0
• Scherrer, W. (1946), " ", Elemente der Mathematik (Birkhäuser) 1 (6): 97–98, ISSN 0013-6018,

External links

• The crystallographic restriction