My watch list

Dielectric function

The dielectric function of a material $ε(ω)$ describes its optical properties at all energies $\hbar\omega$ .

Additional recommended knowledge

Essential Laboratory Skills Guide

Daily Visual Balance Check

What is the Sensitivity of my Balance?

In the case of solids, the complex dielectric function is intimately connected to band structure. The primary quantities that characterize the electronic structure of any crystalline material are its critical-point energies. These are the energies, $E i$ , at which there are discontinuities or infinite first derivatives in the joint density of states or, in the absence of line broadening, in the probability of photon absorption and hence in the imaginary part of the optical dielectric function $ε(ω)$ .

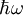The optical dielectric function is given by the fundamental expression $\epsilon(\omega)=1+\frac{8\pi^2e^2}{m^2}\sum_{c,v}\int_{}^{} W_{cv}(E) \left[\phi(\hbar\omega-E)-\phi(\hbar\omega+E) \right ] \, dx$ . In this expression, $W c v (E)$ represents the product of the Brillouin-zone-average transition probability at the energy $E$ and the JDS, $J c v (E)$ ; $φ$ is the broadening function. In general, the broadening is intermediate between Lorentzian and Gaussian; for an alloy it is somewhat closer to Lorentzian because of strong scattering from statistical fluctuations in the local composition on a nanometer scale.