Dispersion (water waves)

Dispersion of water waves generally refers to frequency dispersion. That is, water, in fluid dynamics, is generally considered to be a dispersive medium; which means that the velocity of the wave front travels as a function of frequency so that spatial and temporal phase properties of the wave propagation are constantly changing. So, for example, waves travelling in water with a longer wavelength and period travel faster than those with a shorter wavelength and period. This phenomenon is expressed by the so-called linear dispersion relationship, which may be given as,

.

Additional recommended knowledge

How to ensure accurate weighing results every day?

Essential Laboratory Skills Guide

Guide to balance cleaning: 8 simple steps

Here ω is the angular frequency, g is gravity, k is the wavenumber, and h is the height. The height here refers to the surface wave phenomena and is incorporated into the given form of the dispersion relation. The hyperbolic tangent is meant to physically model the observation that dispersion asymptotically goes to zero as h gets small. Under these assumptions, the linear wave celerity (scalar valued velocity) may then be expressed as,

.

These equations are correct to the second order perturbation theory expansion. To the third order, and for deep water, the dispersion relation is,

.

where A is wave amplitude. This implies that large waves travel faster than small ones of the same frequency. This is only noticeable when the wave amplitude is large.

Historically, this equation . was derived by George Biddell Airy and published in about 1840. A similar equation was also derived by Philip Kelland at around the same time.

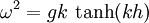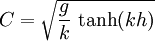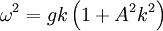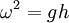This equation is quite frequently approximated to , which was derived by Joseph Louis Lagrange.

See also

• Dispersive partial differential equation