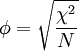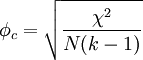To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Effect sizeIn statistics, effect size is a measure of the strength of the relationship between two variables. In scientific experiments, it is often useful to know not only whether an experiment has a statistically significant effect, but also the size of any observed effects. In practical situations, effect sizes are helpful for making decisions. Effect size measures are the common currency of meta-analysis studies that summarize the findings from a specific area of research. Product highlight
SummaryThe concept of effect size appears in everyday language. For example, a weight loss program may boast that it leads to an average weight loss of 30 pounds. In this case, 30 pounds is an indicator of the claimed effect size. Another example is that a tutoring program may claim that it raises school performance by one letter grade. This grade increase is the claimed effect size of the program. An effect size is best explained through an example: if you had no previous contact with humans, and one day visited England, how many people would you need to see before you realize that, on average, men are taller than women there? The answer relates to the effect size of the difference in average height between men and women. The larger the effect size, the easier it is to see that men are taller. If the height difference were small, then it would require knowing the heights of many men and women to notice that (on average) men are taller than women. This example is demonstrated further below. In inferential statistics, an effect size helps to determine whether a statistically significant difference is a difference of practical concern. In other words, given a sufficiently large sample size, it is always possible to show that there is a difference between two means being compared out to some decimal position. The effects size helps us to know whether the difference observed is a difference that matters. Effect size, along with sample size and critical significance level α, and power in statistical hypothesis testing are related, and any one of these values can be determined given the others. In meta-analysis, effect sizes are used as a common measure that can be calculated for different studies and then combined into overall analyses. The term effect size is most commonly used to described standardized measures of effect (e.g., r, Cohen's d, odds ratio, etc.). However, unstandardized measures (e.g., the raw difference between group means, unstandardized regression coefficients, etc.) can equally be effect size measures. Standardized effect size measures are typically used when the metrics of variables being studied do not have intrinsic meaning to the reader (e.g., a score on a personality test on an arbitrary scale), or when results from multiple studies are being combined when some or all of the studies use different scales. Some students mistook the recommendation of Wilkinson & APA Task Force on Statistical Inference (1999, p. 599)--Always present effect sizes for primary outcomes--as that reporting standardized measures of effect like Cohen's d is the default requirement. Actually, just following the sentence the authors added that -- If the units of measurement are meaningful on a practical level (e.g., number of cigarettes smoked per day), then we usually prefer an unstandardized measure (regression coefficient or mean difference) to a standardized measure (r or d). TypesPearson r correlationPearson's r correlation is one of the most widely used effect sizes. It can be used when the data are continuous or binary, thus the Pearson r is arguably the most versatile effect size. This was the first important effect size to be developed in statistics, and it was introduced by Karl Pearson. Pearson's r can vary in magnitude from -1 to 1, with -1 indicating a perfect negative relationship, 1 indicating a perfect positive relationship, and 0 indicating no relationship between two variables. Cohen (1988, 1992) gives the rules of thumb: small = 0.1; medium = 0.3; large = 0.5. Another often used measure of the size of the relationship between two variables is the square of r, often referred to as "r-squared" or the coefficient of determination. It is a measure of the proportion of variance shared by the two variables and varies from 0 to 1. An r² of 0.21 would suggest that 21% of the variance is shared by these two variables. Cohen's dCohen's d is the appropriate effect size measure to use in the context of a t-test on means. d is defined as the difference between two means divided by the pooled standard deviation for those means. Thus, in the case where both samples are the same size,
Different people offer different advice regarding how to interpret the resultant effect size, but the most accepted opinion is that of Cohen (1992) where 0.2 is indicative of a small effect, 0.5 a medium and 0.8 a large effect size. So, in the example above of visiting England and observing men and women's height, the data (Aaron,Kromrey,& Ferron, 1998, November; from a 2004 UK representative sample of 2436 men and 3311 women) is:
The effect size (using Cohen's d) would equal 1.72 (95% confidence intervals: 1.66 - 1.78). This is very large and you should have no problem in detecting that there is a consistent height difference, on average, between men and women. One point worth noting, though, is that in some cases it may be wise to use just one of the standard deviations (e.g., pre-treatment standard deviation in a therapeutic trial). Either way, note that sample size does not play a part in the calculation - points noted by Hedges. Hedges' ĝHedges and Olkin (1985) noted that one could adjust effect size estimates by taking into account the sample size. The problem with Cohen's d is that the outcome is heavily influenced by the denominator in the equation. If one standard deviation is larger than the other then the denominator is weighted in that direction and the effect size is more conservative. However, surely it makes more sense to put stock in the larger sample size? Hedges' ĝ incorporates sample size by both computing a denominator which looks at the sample sizes of the respective standard deviations and also makes an adjustment to the overall effect size based on this sample size. The formula for Hedges' ĝ (as used by software such as the Effect Size Generator) is:
In the above 'height' example, Hedges' ĝ effect size equals 1.76 (95% confidence intervals: 1.70 - 1.82). Notice how the large sample size has increased the effect size from Cohen's d? If, instead, the available data were from only 90 men and 80 women Hedges' ĝ would provide a more conservative estimate of effect size: 1.70 (with larger 95% confidence intervals: 1.35 - 2.05). Cohen's f2Cohen's f2 is the appropriate effect size measure to use in the context of an F-test for multiple correlation or multiple regression. The f2 effect size measure for multiple regression is defined as:
The f2 effect size measure for hierarchical multiple regression is defined as:
By convention, f2 effect sizes of 0.02, 0.15, and 0.35 are considered small, medium, and large, respectively (Cohen, 1988). φ, Cramer's φ, or Cramer's V
The best measure of association for the chi-square test is phi (or Cramer's phi or V). Phi is related to the point-biserial correlation coefficient and Cohen's d and estimates the extent of the relationship between two variables (2 x 2).[1] Cramer's Phi may be used with variables having more than two levels. Phi can be computed by finding the square root of the chi-square statistic divided by the sample size. Similarly, Cramer's phi can be found through a slightly more complex formula that takes the number of rows or columns into account (k). Odds ratioThe odds ratio is another useful effect size. It is appropriate when both variables are binary. For example, consider a study on spelling. In a control group, two students pass the class for every one who fails, so the odds of passing are two to one (or more briefly 2/1 = 2). In the treatment group, six students pass for every one who fails, so the odds of passing are six to one (or 6/1 = 6). The effect size can be computed by noting that the odds of passing in the treatment group are three times higher than in the control group (because 6 divided by 2 is 3). Therefore, the odds ratio is 3. However, odds ratio statistics are on a different scale to Cohen's d. So, this '3' is not comparable to a Cohen's d of '3'. See also
References
Further Explanations
|
|||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Effect_size". A list of authors is available in Wikipedia. |





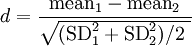
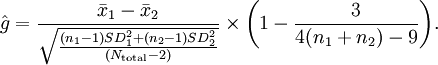
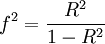
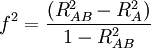
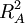 is the variance accounted for by a set of one or more independent variables A, and
is the variance accounted for by a set of one or more independent variables A, and 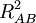 is the combined variance accounted for by A and another set of one or more independent variables B.
is the combined variance accounted for by A and another set of one or more independent variables B.