To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Electrical conductivity
It is also possible to have materials in which the conductivity is anisotropic, in which case σ is a 3×3 matrix (or more technically a rank-2 tensor) which is generally symmetric. Conductivity is the reciprocal (inverse) of electrical resistivity and has the SI units of siemens per metre (S·m-1) i.e. if the electrical conductance between opposite faces of a 1-metre cube of material is 1 siemens then the material's electrical conductivity is 1 siemens per metre. Electrical conductivity is commonly represented by the Greek letter σ, but κ or γ are also occasionally used. An EC meter is normally used to measure conductivity in a solution. Product highlight
Classification of materials by conductivity
The degree of doping in solid state semiconductors makes a large difference in conductivity. More doping leads to higher conductivity. The conductivity of a solution of water is highly dependent on its concentration of dissolved salts and sometimes other chemical species which tend to ionize in the solution. Electrical conductivity of water samples is used as an indicator of how salt-free or impurity-free the sample is; the purer the water, the lower the conductivity. Some electrical conductivities
Complex conductivityTo analyse the conductivity of materials exposed to alternating electric fields, it is necessary to treat conductivity as a complex number (or as a matrix of complex numbers, in the case of anisotropic materials mentioned above) called the admittivity. This method is used in applications such as electrical impedance tomography, a type of industrial and medical imaging. Admittivity is the sum of a real component called the conductivity and an imaginary component called the susceptivity. [1] Temperature dependenceElectrical conductivity is strongly dependent on temperature. In metals, electrical conductivity decreases with increasing temperature, whereas in semiconductors, electrical conductivity increases with increasing temperature. Over a limited temperature range, the electrical conductivity can be approximated as being directly proportional to temperature. In order to compare electrical conductivity measurements at different temperatures, they need to be standardized to a common temperature. This dependence is often expressed as a slope in the conductivity-vs-temperature graph, and can be used: where
The temperature compensation slope for most naturally occurring waters is about 2 %/°C, however it can range between (1 to 3) %/°C. This slope is influenced by the geochemistry, and can be easily determined in a laboratory. At extremely low temperatures (not far from absolute 0 K), a few materials have been found to exhibit very high electrical conductivity in a phenomenon called superconductivity. See also
|
||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Electrical_conductivity". A list of authors is available in Wikipedia. |


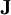 to the electric field strength
to the electric field strength 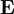 :
:
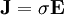 .
.