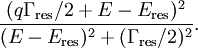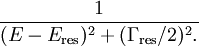My watch list

Fano resonance

In physics, a Fano resonance, in contrast with a Breit–Wigner resonance, is a resonance for which the corresponding profile in the cross-section has the so-called Fano shape, i.e. it can be fitted with a function proportional to:

${(q \Gamma_\mathrm{res}/2 + E - E_\mathrm{res})^2 \over (E - E_\mathrm{res})^2 + (\Gamma_\mathrm{res}/2)^2 }.$

Additional recommended knowledge

What is the Sensitivity of my Balance?

Don't let static charges disrupt your weighing accuracy

Better weighing performance in 6 easy steps

The $E res$ and $Γ res$ parameters are the standard Breit–Wigner parameters (position and width of the resonance, respectively). The q parameter is the so-called Fano parameter. It is interpreted (within the Feshbach–Fano partitioning theory) as the ratio between the resonant and direct (background) scattering probability. In the case the direct scattering probability is vanishing, the q parameter becomes infinite and the Fano formula is boiling down to the usual Breit–Wigner (Lorentzian) formula:

$1 \over (E - E_\mathrm{res})^2 + (\Gamma_\mathrm{res}/2)^2.$