My watch list

Fin (extended surface)

In the study of heat transfer, a fin is a surface that extends from an object to increase the rate of heat transfer to or from the environment by increasing convection. The amount of conduction, convection, or radiation of an object determines the amount of heat it transfers. Increasing the temperature difference between the object and the environment, increasing the convection heat transfer coefficient, or increasing the surface area of the object increases the heat transfer. Sometimes it is not economical or it is not feasible to change the first two options. Adding a fin to an object, however, increases the surface area and can sometimes be an economical solution to heat transfer problems.

Additional recommended knowledge

Weighing the right way

Better weighing performance in 6 easy steps

Don't let static charges disrupt your weighing accuracy

1 Simplified Case
2 Four Uniform Cross-sectional Area Cases
3 Fin Performance
4 Fin Uses
5 References

Simplified Case

To create a simplified equation for the heat transfer of a fin, many assumptions need to be made.

Assume:

Steady state
Constant material properties (independent of temperature)
No heat transfer
No internal heat generation
One-dimensional conduction
Uniform cross-sectional area
Uniform convection across the surface area

With these assumptions, the conservation of energy can be used to create an energy balance for a differential cross section of the fin.^[1]

$q_x=q_{x+dx}+dq_{conv}\,$

Fourier’s law states that

$q_x=-kA_c \left ( \frac{dT}{dx} \right )$ ,

where $A c$ is the cross-sectional area of the differential element.^[2] Therefore the conduction rate at x+dx can be expressed as

$q_{x+dx}=q_x+\left ( \frac{dq_x}{dx} \right )dx$

Hence, it can also be expressed as

$q_{x+dx}=-kA_c\left ( \frac{dT}{dx} \right )-k\frac{d}{dx} \left ( A_c\frac{dT}{dx} \right )dx$ .

Since the equation for heat flux is

$q''=h\left (T_s-T_\infty\right )$

then $d q c o n v$ is equal to

$h*dA_s \left(T-T_\infty\right)$

where $A s$ is the surface area of the differential element. By substitution it is found that

$\frac{d^2T}{dx^2} = \left (\frac{1}{A_c}\frac{dA_c}{dx} \right )\frac{dT}{dx} - \left (\frac{1}{A_c} \frac{h}{k} \frac{dA_s}{dx} \right ) \left ( T - T_\infty \right )$

This is the general equation for convection from extended surfaces. Applying certain boundary conditions will allow this equation to simplify.

Four Uniform Cross-sectional Area Cases

For all four cases, the above equation will simplify because the area is constant and

$\frac {dA_s}{dx} = P$

where P is the perimeter of the cross-sectional area. Thus, the general equation for convection from extended surfaces with constant cross-sectional area simplifies to

$\frac{d^2T}{dx^2}=\frac{hP}{kA_c}\left(T-T_\infty\right)$ .

The solution to the simplified equation is

$θ(x) = C 1 e m x + C 2 e - m x$

where $m^2=\frac{hP}{kA_c}$

and $\theta_x=T(x)-T_\infty$ .

The constants $C 1$ and $C 2$ can be found by applying the proper boundary conditions. All four cases have the boundary condition $T (x = 0) = T b$ for the temperature at the base. The boundary condition at $x = L$ , however, is different for all of them, where L is the length of the fin.

For the first case, the second boundary condition is that there is free convection at the tip. Therefore,

$hA_c\left(T(L)-T_\infty\right)=-kA_c\left.\left(\frac{dT}{dx}\right)\right\vert_{x=L}$

which simplifies to

$h\theta(L)=-k\left.\frac{d\theta}{dx}\right\vert_{x=L}$

Knowing that

$\theta_b=T_{base}-T_\infty$ ,

the equations can be combined to produce

$h\left(C_1e^{mL}+C_2e^{-mL}\right)=km\left(C_2e^{-mL}-C_1e^{mL}\right)$

$C 1$ and $C 2$ can be solved to produce the temperature distribution, which is in the table below. Then applying Fourier’s law at the base of the fin, the heat transfer rate can be found.

Similar mathematical methods can be used to find the temperature distributions and heat transfer rates for other cases. For the second case, the tip is assumed to be adiabatic or completely insulated. Therefore at x=L,

$\frac{d\theta}{dx}=0$

because heat flux is 0 at an adiabatic tip. For the third case, the temperature at the tip is held constant. Therefore the boundary condition is

$θ(L) = θ L$ . For the fourth and final case, the fin is assumed to be infinitely long. Therefore the boundary condition is

$\lim_{L\rightarrow \infty} \theta_L=0\,$ .

The temperature distributions and heat transfer rates can then be found for each case.

Temperature Distribution and Heat Transfer Rate for Fins of Uniform Cross Sectional Area
Case	Tip Condition (x=L)	Temperature Distribution	Fin Heat Transfer Rate
A	Convection heat transfer	$\frac{\theta}{\theta_b}=\frac{\cosh{m(L-x)}+\left(\frac{h}{mk}\right)\sinh {m(L-x)}}{\cosh{mL}+\left(\frac{h}{mk}\right)\sinh{mL}}$	$\sqrt{hPkA_c}\theta_b\frac{\sinh {mL} + (h/mk) \cosh {mL}}{\cosh {mL} + (h/mk) \sinh {mL}}$
B	Adiabatic	$\frac{\theta}{\theta_b}=\frac{\cosh {m(l-x)}}{\cosh {mL}}$	$\sqrt{hPkA_c}\theta_b\tanh {mL}$
C	Constant Temperature	$\frac{\theta}{\theta_b}=\frac{\frac{\theta_L}{\theta_b}\sinh {mx} + \sinh {m(L-x)}}{\sinh {mL}}$	$\sqrt{hPkA_c}\theta_b\frac{\cosh {mL} - frac{\theta_L}{\theta_b}}{\sinh {mL}}$
D	Infinite Fin Length	$\frac{\theta}{\theta_b}=e^{-mx}$	$\sqrt{hPkA_c}\theta_b$

Fin Performance

Fin performance can be described in three different ways. The first is fin effectiveness. It is the ratio of the fin heat transfer rate to the heat transfer rate of the object if it had no fin. The formula for this is

$εf = fracqfhAc,bθb$ ,

where $A c, b$ is the fin cross-sectional area at the base. Fin performance can also be characterized by fin efficiency. This is the ratio of the fin heat transfer rate to the heat transfer rate of the fin if the entire fin were at the base temperature.

$η f = q f h A f θ b$

$A f$ in this equation is equal to the surface area of the fin. Fin efficiency will always be less than one. This is because assuming the temperature throughout the fin is at the base temperature would increase the heat transfer rate. The third way fin performance can be described is with overall surface efficiency.

$\eta_o=\frac{q_t}{hA_t\theta_b}$ ,

where $A t$ is the total area and $q t$ is the sum of the heat transfer rates of all the fins. This is the efficiency for an array of fins.

Fin Uses

Fins are most commonly used in heat exchanging devices such as radiators in cars and heat exchangers in power plants.^[3]^[4] They are also used in newer technology such as hydrogen fuel cells.^[5] Nature has also taken advantage of the phenomena of fins. The ears of jackrabbits act as fins to release heat from the blood that flows through them.^[6]

References

Incropera, Frank; DeWitt, David P., Bergman, Theodore L., Lavine, Adrienne S. (2007). Fundamentals of Heat and Mass Transfer, Sixth Edition, New York: John Wiley & Sons, 2-168. ISBN 0-471-45728-0.

Category: Convection

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fin_(extended_surface)". A list of authors is available in Wikipedia.
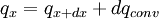
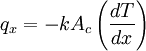
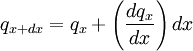
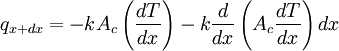
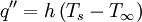
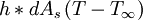
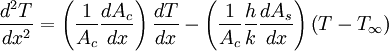
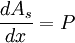
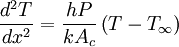
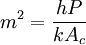
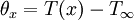
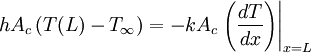
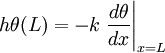
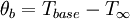
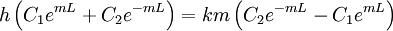
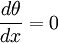
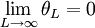
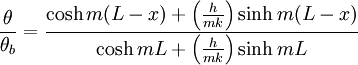
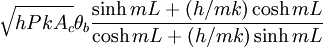
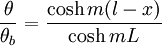
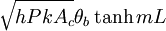
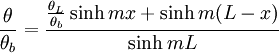
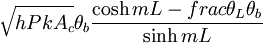
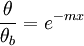
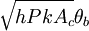
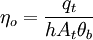