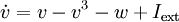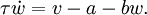My watch list

FitzHugh-Nagumo model

The FitzHugh-Nagumo Model (named after Richard FitzHugh, 1922-2007) describes a prototype of an excitable system, i.e., a neuron.

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

What is the Sensitivity of my Balance?

Daily Sensitivity Test

If the external stimulus $I ext$ exceeds a certain threshold value, the system will exhibit a characteristic excursion in phase space, before the variables $v$ and $w$ relax back to their rest values.

This behaviour is typical for spike generations (=short elevation of membrane voltage $v$ ) in a neuron after stimulation by an external input current.

The equations for this dynamical system read

$\dot{v}=v-v^3 - w + I_{\rm ext}$

$\tau \dot{w} = v-a-b w.$

The dynamics of this system can be nicely described by zapping between the left and right branch of the cubic nullcline.

The FitzHugh-Nagumo model is a simplified version of the Hodgkin-Huxley model which models in a detailed manner activation and deactivation dynamics of a spiking neuron. In the original papers of FitzHugh this model was called Bonhoeffer-van der Pol oscillator, since it contains the van der Pol oscillator as a special case for $a = b = 0$ .

References

FitzHugh R. (1955) Mathematical models of threshold phenomena in the nerve membrane. Bull. Math. Biophysics, 17:257--278
FitzHugh R. (1961) Impulses and physiological states in theoretical models of nerve membrane. Biophysical J. 1:445-466
FitzHugh R. (1969) Mathematical models of excitation and propagation in nerve. Chapter 1 (pp. 1-85 in H.P. Schwan, ed. Biological Engineering, McGraw-Hill Book Co., N.Y.)
Nagumo J., Arimoto S., and Yoshizawa S. (1962) An active pulse transmission line simulating nerve axon. Proc IRE. 50:2061–2070.

Category: Electrophysiology