My watch list

Forest-fire model

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

Don't let static charges disrupt your weighing accuracy

Daily Sensitivity Test

In applied mathematics, a forest-fire model is any of a number of dynamical systems displaying self-organized criticality. Note, however, that according to Pruessner et al. (2002, 2004) the forest-fire model does not behave critically on very large, i.e. physically relevant scales. Early versions go back to Henley (1989) and Drossel and Schwabel (1992). The model is defined as a cellular automaton on a grid with L^d cells. L is the sidelength of the grid and d is its dimension. A cell can be empty, occupied by a tree, or burning. The model of Drossel and Schwabl (1992) is defined by four rules which are executed simultaneously:

A burning cell turns into an empty cell
A tree will burn if at least one neighbor is burning
A tree ignites with probability f even if no neighbor is burning
An empty space fills with a tree with probability p

The controlling parameter of the model is p/f which gives the average number of trees planted between two lightning strikes (see Schenk et al. (1996) and Grassberger (1993)). In order to exhibit a fractal frequency-size distribution of clusters a double separation of time scales is necessary

$f \ll p \ll T_\mathrm{smax}\,$

where T_smax is the burn time of the largest cluster. The scaling behavior is not simple, however (Grassberger 1993,2002 and Pruessner et al. 2002,2004).

A cluster is defined as a coherent set of cells, all of which have the same state. Cells are coherent if they can reach each other via nearest neighbor relations. In most cases, the von Neumann neighborhood (four adjacent cells) is considered.

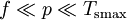
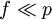The first condition $f\ll p$ allows large structures to develop, while the second condition 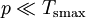$p\ll T_\mathrm{smax}$ keeps trees from popping up alongside a cluster while burning.

References

Bak, P., Chen, K. and Tang, C. (1990), "A forest-fire model and some thoughts on turbulence." Phys. Lett. A 147, 297–300.
Chen, K., Bak, P. and Jensen, M. H. (1990), "A deterministic critical forest-fire model." Phys. Lett. A 149, 207–210.
Drossel, B. and Schwabl, F. (1992), "Self-organized critical forest-fire model." Phys. Rev. Lett. 69, 1629–1632.
Grassberger, P. (2002), "Critical behaviour of the Drossel-Schwabl forest fire model." New J. Phys. 4, 17.
Henley, C. L. (1989), "Self-organized percolation: a simpler model." Bull. Am. Phys. Soc. 34, 838.
Henley, C. L. (1993), "Statics of a 'self-organized' percolation model." Phys. Rev. Lett. 71, 2741–2744.