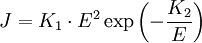Fowler-Nordheim equation

The Fowler-Nordheim equation in solid state physics relates current, work and electric field strength to determine field emission. It has two parts: an equation for field emitted current density, and the equation for total current. It is named after Ralph H. Fowler and Lothar W. Nordheim.

Additional recommended knowledge

What is the Sensitivity of my Balance?

Daily Sensitivity Test

Recognize and detect the effects of electrostatic charges on your balance

The current density flowing through a thin oxide layer due to Fowler-Nordheim tunneling is a function of the electric field across the oxide. The electric field is the voltage divided by the distance. This article describes how quickly current increases with voltage.

V = voltage, volts

t = thickness of oxide, meters

E = V/t electric field, volts per meter

I = current, amperes

A = area of oxide, square meters

J = I/A

J = current density in amperes per square meter

K₁ is a constant described in the reference

K₂ is a second constant, also described in the reference

For the Fowler-Nordheim tunneling current density :

The point is that the current increases with the voltage squared multiplied by an exponential increase with inverse voltage. While the second factor, E², obviously increases rapidly with voltage, the third factor, the exponential, deserves another sentence. For people who are not familiar with exponentials of negative inverses, the following sentences are helpful.

Assume, temporarily, that K₂ is normalized to be 1.

The factor e^-1/E increases with E. If E is near zero, the exponent is large, and exp(-large) is near zero.

If E is large, 1/E is small, and almost zero: exp(0) = 1

Therefore, exp(-1/E) gets larger as E gets larger, since one is greater than zero. Ultimately, this third factor will maintain a value between zero and one.

Conclusion

J increases by two voltage-related factors that are multiplied: (exponentially with voltage) x (squared with voltage)