To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Galton-Watson processThe Galton-Watson process is a stochastic process arising from Francis Galton's statistical investigation of the extinction of surnames. Product highlight
History
There was concern amongst the Victorians that aristocratic surnames were becoming extinct. Galton originally posed the question regarding the probability of such an event in the Educational Times of 1873, and the Reverend Henry William Watson replied with a solution. Together, they then wrote an 1874 paper entitled On the probability of extinction of families. However, the concept was previously discussed by I. J. Bienaymé; see Heyde and Seneta 1977; though it appears that Galton and Watson derived their process independently. For a detailed history see Kendall (1966 and 1975). ConceptsAssume, as was taken for granted in Galton's time, that surnames are passed on to all male children by their father. Suppose the number of a man's sons to be a random variable distributed on the set { 0, 1, 2, 3, ...}. Further suppose the numbers of different men's sons to be independent random variables, all having the same distribution. Then the simplest substantial mathematical conclusion is that if the average number of a man's sons is 1 or less, then their surname will surely die out, and if it is more than 1, then there is more than zero probability that it will survive forever. Modern applications include the survival probabilities for a new mutant gene, or the initiation of a nuclear chain reaction, or the dynamics of disease outbreaks in their first generations of spread, or the chances of extinction of small population of organisms; as well as explaining (perhaps closest to Galton's original interest) why only a handful of males in the deep past of humanity now have any surviving male-line descendants, reflected in a rather small number of distinctive human Y-chromosome DNA haplogroups. A corollary of high extinction probabilities is that if a lineage has survived, it is likely to have experienced, purely by chance, an unusually high growth rate in its early generations at least when compared to the rest of the population. Mathematical definitionA Galton-Watson process is a stochastic process {Xn} which evolves according to the recurrence formula X0 = 1 and where for each n, and is equal to one if E{ξ1} ≤ 1 and strictly less than one if E{ξ1} > 1. The process can be treated analytically using the method of probability generating functions. If the number of children ξ j at each node follows a Poisson distribution, a particularly simple recurrence can be found for the total extinction probability xn for a process starting with a single individual at time n = 0: giving the curves plotted above. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Galton-Watson_process". A list of authors is available in Wikipedia. |





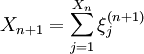
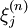 is a sequence of IID natural number-valued random variables. The extinction probability is given by
is a sequence of IID natural number-valued random variables. The extinction probability is given by