To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gross-Pitaevskii equationThe Gross-Pitaevskii equation is a nonlinear model equation for the order parameter or wavefunction of a Bose-Einstein condensate. It is similar in form to the Ginzburg-Landau equation and is sometimes referred to as a nonlinear Schrödinger equation. A Bose-Einstein condensate (BEC) is a gas of bosons that are in the same quantum state, and thus can be described by the same wavefunction. A free quantum particle is described by a single-particle Schrödinger equation. Interaction between particles in a real gas is taken into account by a pertinent many-body Schrödinger equation. If the average spacing between the particles in a gas is greater than the scattering length (that is, in the so-called dilute limit), then one can approximate the true interaction potential that features in this equation by a pseudopotential. The non-linearity of the Gross-Pitaevskii equation has its origin in the interaction between the particles. This becomes evident by equating the coupling constant of interaction, Product highlight
Form of EquationThe equation has the form of the Schrödinger equation with the addition of an interaction term. The coupling constant, g, is proportional to the scattering length of two interacting bosons:
where where Ψ is the wavefunction, or order parameter, and V is an external potential. The time-independent Gross-Pitaevskii equation, for a conserved number of particles, is where μ is the chemical potential. The chemical potential is found from the condition that the number of particles is related to the wavefunction by
From the time-independent Gross-Pitaevskii equation, we can find the structure of a Bose-Einstein condensate in various external potentials (e.g. a harmonic trap). The time-dependent Gross-Pitaevskii equation is
From the time-dependent Gross-Pitaevskii equation we can look at the dynamics of the Bose-Einstein condensate. It is used to find the collective modes of a trapped gas. SolutionsSince the Gross-Pitaevskii equation is a nonlinear, partial differential equation, exact solutions are hard to come by. As a result, solutions have to be approximated via a myriad of techniques. Exact SolutionsFree ParticleThe simplest exact solution is the free particle solution, with
This solution is often called the Hartree solution. Although it does satisfy the Gross-Pitaevskii equation, it leaves a gap in the energy spectrum due to the interaction:
According to the Hugenholtz-Pines theorem,[1] an interacting bose gas does not exhibit an energy gap (in the case of repulsive interactions). SolitonA one-dimensional soliton can form in a Bose-Einstein condensate, and depending upon whether the interaction is attractive or repulsive, there is either a light or dark soliton. Both solitons are local disturbances in a condensate with a uniform background density If the BEC is repulsive, so that g > 0, then a possible solition of the Gross-Pitaevskii equation is,
where ψ0 is the value of the condensate wavefuntion at For g < 0 where the chemical potential is 1-D Square Well PotentialVariational SolutionsIn systems where an exact analytical solution may not be feasible, one can make a variational approximation. The basic idea is to make a variational ansatz for the wavefunction with free parameters, plug it into the free energy, and minimize the energy with respect to the free parameters. Thomas-Fermi ApproximationBogoliubov ApproximationNotes
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gross-Pitaevskii_equation". A list of authors is available in Wikipedia. |


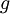 , in the Gross-Pitaevskii equation with zero (see the following section), on which the single-particle Schrödinger equation describing a particle inside a trapping potential is recovered.
, in the Gross-Pitaevskii equation with zero (see the following section), on which the single-particle Schrödinger equation describing a particle inside a trapping potential is recovered.



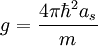 ,
,
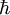 is Planck's constant and m is the mass of the boson.
The energy density is
is Planck's constant and m is the mass of the boson.
The energy density is
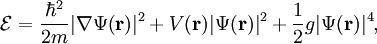
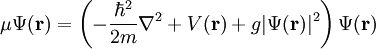
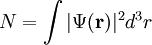 .
.
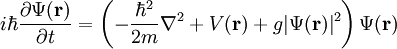 .
.
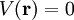 ,
,
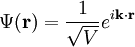 .
.
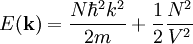 .
.
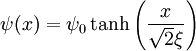 ,
,
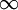 , and
, and 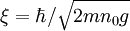 , is the coherence length. This solution represents the dark soliton, since there is a deficit of condensate in a space of nonzero density. The dark soliton is also a type of topological defect, since
, is the coherence length. This solution represents the dark soliton, since there is a deficit of condensate in a space of nonzero density. The dark soliton is also a type of topological defect, since ![\psi(x,t) = \psi(0)e^{-i\mu t/\hbar}\frac{1}{\cosh\left[\sqrt{2m\vert\mu\vert/\hbar^2}x\right]},](images/math/6/d/e/6de1b30b64636afa9c168bd00305bfe4.png)
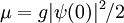 . This solution represents the bright soliton, since there is a concentration of condensate in a space of zero density.
. This solution represents the bright soliton, since there is a concentration of condensate in a space of zero density.


