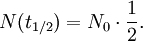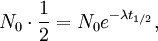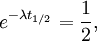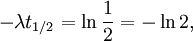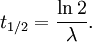To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Half-lifeThe half-life of a quantity whose value decreases with time is the interval required for the quantity to decay to half of its initial value. The concept originated in the study of radioactive decay which is subject to exponential decay but applies to all phenomena including those which are described by non-exponential decays. The term half-life was coined in 1907, but it was always referred to as half-life period. It was not until the early 1950s that the word period was dropped from the name. [1]
The table at right shows the reduction of the quantity in terms of the number of half-lives elapsed. It can be shown that, for exponential decay, the half-life t1 / 2 obeys this relation: where
The half-life is related to the mean lifetime τ by the following relation: Product highlight
ExamplesThe constant λ can represent many different specific physical quantities, depending on what process is being described.
Decay by two or more processesSome quantities decay by two processes simultaneously (see Decay by two or more processes). In a fashion similar to the previous section, we can calculate the new total half-life T1 / 2 and we'll find it to be: or, in terms of the two half-lives t1 and t2 i.e., half their harmonic mean. Simple Formulam(t) mass left depending on time. m(0) = initial mass t = time passed h = half life of the object DerivationQuantities that are subject to exponential decay are commonly denoted by the symbol N. (This convention suggests a decaying number of discrete items. This interpretation is valid in many, but not all, cases of exponential decay.) If the quantity is denoted by the symbol N, the value of N at a time t is given by the formula: where N0 is the initial value of N (at t = 0) When t = 0, the exponential is equal to 1, and N(t) is equal to N0. As t approaches infinity, the exponential approaches zero. In particular, there is a time Substituting into the formula above, we have Experimental determinationThe half-life of a process can be determined easily by experiment. In fact, some methods do not require advance knowledge of the law governing the decay rate, be it exponential decay or another pattern. Most appropriate to validate the concept of half-life for radioactive decay, in particular when dealing with a small number of atoms, is to perform experiments and correct computer simulations. See in [1] how to test the behavior of the last atoms. Validation of physics-math models consists in comparing the model's behavior with experimental observations of real physical systems or valid simulations (physical and/or computer). The references given here describe how to test the validity of the exponential formula for small number of atoms with simple simulations, experiments, and computer code. In radioactive decay, the exponential model does not apply for a small number of atoms (or a small number of atoms is not within the domain of validity of the formula or equation or table). The DIY experiments use pennies or M&M's candies. [2], [3]. A similar experiment is performed with isotopes of a very short half-life, for example, see Fig 5 in [4]. See how to write a computer program that simulates radioactive decay including the required randomness in [5] and experience the behavior of the last atoms. Of particular note, atoms undergo radioactive decay in whole units, and so after enough half-lives the remaining original quantity becomes an actual zero rather than asymptotically approaching zero as with continuous systems. See also
References
Categories: Radioactivity | Chemical kinetics |
||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Half-life". A list of authors is available in Wikipedia. |


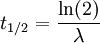
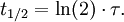



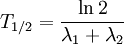
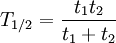
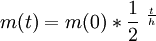
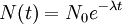
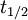 such that
such that