To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Index ellipsoidThe index ellipsoid is a diagram of an ellipsoid that depicts the orientation and relative magnitude of refractive indices in a crystal. Product highlightThe equation for the ellipsoid is constructed using the electric displacement vector, D, and the dielectric constants. Defining the field energy, W, as: and the reduced displacement as: then the index ellipsoid is defined by the equation,
The semiaxes of this ellipsoid are dielectric constants of the crystal. This ellipsoid can be used to determine the polarization of an incoming wave, with wave vector, s, by taking the intersection of the plane Uniaxial indicatrixAn important special case of the index ellipsoid occurs when the ellipsoid is an ellipsoid of revolution, e.g. constructed by rotating an ellipse around either the minor or major axis. In this case, there is only one optical axis; the axis of rotation. In such a case, the material is uniaxial and has only one principal symmetry axis. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Index_ellipsoid". A list of authors is available in Wikipedia. |





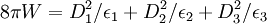
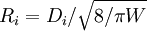
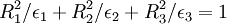 .
.
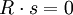 with the index ellipsoid. The axes of the resulting ellipse are the resulting polarization directions.
with the index ellipsoid. The axes of the resulting ellipse are the resulting polarization directions.


