To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Inverse scattering transformIn mathematics, the inverse scattering transform is a procedure for integrating certain nonlinear partial differential equations (PDEs) by first converting them into a system of linear ordinary differential equations (ODEs). The basic idea is not unlike the Fourier transform. It applies to "potentials" (see below for an example) that are rapidly decaying at infinity. Product highlightThe inverse scattering transform may be applied to many of the so-called exactly solvable models. These include the Korteweg-de Vries equation, the nonlinear Schrödinger equation, the coupled nonlinear Schrödinger equations, the Sine-Gordon equation, and the Dym equation. Solutions typically consist of solitons plus some background radiation decaying to zero as time goes to infinity, and are characterized by having non-obvious and un-intuitive constants of motion. The inverse scattering problem can be written as a Riemann-Hilbert factorization problem. Such a "modern" formulation can be generalized to differential operators of order greater than two, but also to the case of periodic potentials. Method of solutionStep 1. Determine the nonlinear partial differential equation. This is usually accomplished by analyzing the physics of the situation being studied. Step 2. Employ forward scattering. This consists of finding the Lax pair. The Lax pair consists of two linear operators, L and M, such that Lv = λv and vt = Mv. It is extremely important that the eigenvalue λ be independent of time; i.e. λt = 0. Necessary and sufficient conditions for this to occur are determined as follows: take the time derivative of Lv = λv to obtain
Plugging in Mv for vt yields
Rearranging on the far right term gives us
Thus,
Since
This is Lax's equation. One important thing to note about Lax's equation is that Lt is the time derivative of L precisely where it explicitly depends on t. The reason for defining the differentiation this way is motivated by the simplest instance of L, which is the Schrödinger operator (see Schrödinger equation): where u is the "potential". Comparing the expression Ltv + Lvt with After concocting the appropriate Lax pair it should be the case that Lax's equation recovers the original nonlinear PDE. Step 3. Determine the time evolution of the eigenvalues λ, the norming constants, and the reflection coefficient, all three comprising the so-called scattering data. This is all a linear process, though complicated. Step 4. Perform the inverse scattering procedure by solving the Marchenko equation, a linear integral equation, to obtain the final solution of the original nonlinear PDE. All the scattering data is required in order to do this. Note that if the reflection coefficient is zero, the process becomes much easier. Note also that this step works if L is a differential or difference operator of order two, but not necessarily for higher orders. In all cases however, the inverse scattering problem is reducible to a Riemann-Hilbert factorization problem. (See Ablowitz-Clarkson (1991) for either approach.) References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Inverse_scattering_transform". A list of authors is available in Wikipedia. |





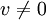 , this implies that
, this implies that 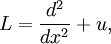
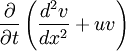 shows us that
shows us that 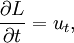 thus ignoring the first term.
thus ignoring the first term.


