To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
JelliumJellium is the model of interacting electrons in which a uniform background of positive charge exists. In this model at zero temperature the system properties are dependent only on the charge density of electrons. This allows for the simplistic calculation of the electron-electron coupling energy being a ratio between the free-electron kinetic energy and the Coulomb potential energy. Product highlightThe model works with the atoms as if they were actually blobs of jelly, hence the name.
The Hamiltonian of the system consists of three parts: With this Hamiltonian and the principles of quantum-mechanics, the energy of the system can be calculated, for example in the approximation of Hartree-Fock or in the theory of Bohm and Pines. The jellium model is also used in nuclear physics, and has been used to try to explain the properties of superatoms. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Jellium". A list of authors is available in Wikipedia. |





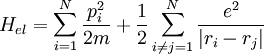 , with:
, with: 

