To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Koide formulaThis unexplained relation was discovered by Yoshio Koide in 1981, and relates the masses of the three leptons so well that it predicted the mass of the tau lepton. Product highlightLet
It is clear that 1 / 3 < Q < 1 from the definition. The superior bound follows if we assume that the square roots can not be negative; R. Foot remarked that 1 / 3Q can be interpreted as the cosine squared of the angle between the vector The mystery is in the physical value. The masses of the electron, muon, and tau lepton are measured respectively as
Not only is this result odd in that three apparently random numbers should give a simple fraction, but also that Q is exactly halfway between the two extremes of 1/3 and 1. This result has never been explained or understood. ReferencesPhys. Rev. D 28, 252–254 (1983) Physics Letters B, Volume 120, Issues 1-3 , 6 January 1983, Pages 161-165 Further readingThe Strange Formula of Dr Koide - A review of the history of the Koide Formula |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Koide_formula". A list of authors is available in Wikipedia. |





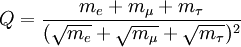
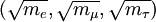 and
and 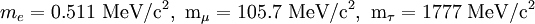 , which gives
, which gives