To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Kramers-Kronig relationThe Kramers-Kronig relations are mathematical properties which connect the real and imaginary parts of any complex function analytic in the upper half plane. These relations are often used to relate the real and imaginary parts of response functions in physical systems because causality implies the analyticity condition is satisfied and conversely.[1] The relation is named in honor of Ralph Kronig[2] and Hendrik Anthony Kramers.[3] Product highlight
DefinitionFor a function χ(ω) = χ1(ω) + iχ2(ω) analytic in the upper half plane which vanishes as and
where DerivationThe proof begins with an application of the residue theorem for complex integration. Given any analytic function χ(ω) in the upper half plane, consider the integral
The contour encloses the upper half plane at infinity, the real axis and a hump over the pole at ω = ω' leaving no poles inside, and so the integral vanishes. We decompose the integral into its contributions along each of the three contour segments. The segment at infinity vanishes since we assume χ(ω) vanishes as we take
Rearranging, we arrive at the compact form of the Kramers-Kronig relations,
The single i in the denominator hints at the connection between the real and imaginary components. Finally, split χ(ω) and the equation into their real and imaginary parts to obtain the forms quoted above. Physical Interpretation and Alternate FormWe can apply the Kramers-Kronig formalism to response functions. In physics, the response function χ(t − t') describes how some property P(t) of a physical system responds to an applied force F(t'). For example, P(t) could be the angle of a pendulum and F(t) the applied force of a motor driving the pendulum motion. The response χ(t − t') must be zero for t < t' since a system cannot respond to a force before it is applied. It can be shown that this causality condition implies the Fourier transform χ(ω) is analytic in the upper half plane. Additionally, if we subject a system to high frequency oscillatory forcing, there will be no time for the system to respond before the forcing has switched direction, and so χ(ω) vanishes as ω becomes large. From these physical considerations, we see that χ(ω) satisfies conditions needed for the Kramers-Kronig relations to apply. The Kramers-Kronig relations have a physical interpretation. The imaginary part of a response function describes how a system dissipates energy, since it is out of phase with the driving force. The Kramers-Kronig relations imply that observing the dissipative response of a system is sufficient to determine its in-phase (reactive) response, and vice versa. The formulas above are not useful for reconstructing physical responses, as the integrals run from Using these properties, we can collapse the integration ranges to
Since χ2(ω) is odd, the second integral vanishes, and we are left with
The same derivation for the imaginary part gives
These are the Kramers-Kronig relations useful for physical response functions. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Kramers-Kronig_relation". A list of authors is available in Wikipedia. |





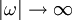 , the Kramers-Kronig relations are given by
, the Kramers-Kronig relations are given by
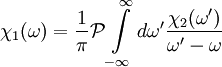
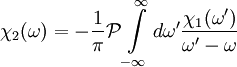 ,
,
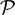 denotes the Cauchy principal value. We see that the real and imaginary parts of such a function are not independent, so that the full function can be reconstructed given just one of its parts.
denotes the Cauchy principal value. We see that the real and imaginary parts of such a function are not independent, so that the full function can be reconstructed given just one of its parts.
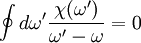 .
.
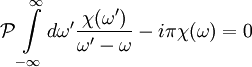 .
.
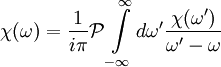 .
.
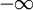 to
to 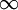 , implying we know the response at negative frequencies. Fortunately, in most systems, the positive frequency-response determines the negative-frequency response because
, implying we know the response at negative frequencies. Fortunately, in most systems, the positive frequency-response determines the negative-frequency response because 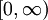 . Consider the first relation giving the real part
. Consider the first relation giving the real part 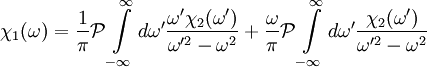 .
.
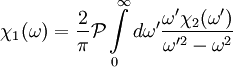 .
.
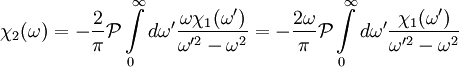 .
.


