Lagrangian and Eulerian coordinates

In fluid dynamics and finite-deformation plasticity the Lagrangian reference frame is a way of looking at fluid motion where the observer follows individual fluid particles as they move through space and time. Plotting the position of an individual particle through time gives the pathline of the particle. This can be visualized by sitting in a boat and drifting down a river.

Additional recommended knowledge

Essential Laboratory Skills Guide

Guide to balance cleaning: 8 simple steps

Daily Sensitivity Test

The Eulerian reference frame is a way of looking at fluid motion that focuses on specific locations in the space through which the fluid flows. This can be visualized by sitting on the bank of a river and watching the water pass the fixed location.

The Lagrangian and Eulerian reference frames are related by the substantial derivative (also called the Lagrangian derivative or the material derivative):

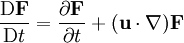
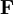This tells us that the total rate of change of some vector function as the particles moves through a flow field described by 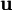is equal to the sum of the local rate of change and convective rate of change of .

See also

• Streamlines, Streaklines and Pathlines
• Fluid dynamics
• Coordinate system