To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Lambert's cosine law
Lambert's cosine law in optics says that the radiant intensity observed from a "Lambertian" surface is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. The law is also known as the cosine emission law or Lambert's emission law. It is named after Johann Heinrich Lambert, from his Photometria, published in 1760. Product highlightAn important consequence of Lambert's cosine law is that when a surface is viewed from any angle, it has the same apparent radiance. This means, for example, that to the human eye it has the same apparent brightness (or luminance). It has the same radiance because, although the emitted power from a given area element is reduced by the cosine of the emission angle, the size of the observed area is increased by a corresponding amount, so that while the area element appears the same in reality it has increased by the cosine of the angle and therefore its radiance is the same. For example, in the visible spectrum, the Sun is almost a perfect Lambertian radiator, and as a result the brightness of the Sun is almost the same everywhere on an image of the solar disk even though we see it full-on only in the center of the disk. Also, a black body is a perfect Lambertian radiator. Lambertian scatterersWhen an area element is radiating as a result of being illuminated by an external source, the irradiance (energy or photons/time/area) landing on that area element will be proportional to the cosine of the angle between the illuminating source and the normal. A Lambertian scatterer will then scatter this light according to the same cosine law as a Lambertian emitter. This means that although the radiance of the surface depends on the angle from the normal to the illuminating source, it will not depend on the angle from the normal to the observer. For example, if the moon were a Lambertian scatterer, one would expect to see its scattered brightness appreciably diminish towards the terminator due to the increased angle at which sunlight hit the surface. The fact that it does not diminish illustrates that the moon is not a Lambertian scatterer, and in fact tends to scatter more light into the oblique angles than would a Lambertian scatterer. Details of equal brightness effectThe situation for a Lambertian surface (emitting or scattering) is illustrated in Figures 1 and 2. For conceptual clarity we will think in terms of photons rather than energy or luminous energy. The wedges in the circle each represent an equal angle d Ω and, for a Lambertian surface, the number of photons per second emitted into each wedge is proportional to the area of the wedge. It can be seen that the length of each wedge is the product of the diameter of the circle and cos(θ). It can also be seen that the maximum rate of photon emission per unit solid angle is along the normal and diminishes to zero for θ = 90°. In mathematical terms, the radiance along the normal is I photons/(s·cm2·sr) and the number of photons per second emitted into the vertical wedge is I dΩ dA. The number of photons per second emitted into the wedge at angle θ is I cos(θ) dΩ dA. Figure 2 represents what an observer sees. The observer directly above the area element will be seeing the scene through an aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0. We can assume without loss of generality that the aperture happens to subtend solid angle dΩ when "viewed" from the emitting area element. This normal observer will then be recording I dΩ dA photons per second and so will be measuring a radiance of
The observer at angle θ to the normal will be seeing the scene through the same aperture of area dA0 and the area element dA will subtend a (solid) angle of dΩ0 cos(θ). This observer will be recording I cos(θ) dΩ dA photons per second, and so will be measuring a radiance of
which is the same as the normal observer. |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lambert's_cosine_law". A list of authors is available in Wikipedia. |
- Green methanol for shipping and industry: € 10.4 Mio. for the "Leuna100" project - A consortium of two Fraunhofer institutes, DBI-Gastechnologisches Institut Freiberg, Technical University of Berlin and C1 makes industrial history at the Leuna site
- New device uses carbon nanotubes to snag molecules
- The bat is the godfather of digital transformation - Saving resources with the virtual paint lab
- A thoroughly modern magnesium process
- Batteries: Modeling tomorrow's materials today - Microstructure simulations reveal strong influence of elastic deformations on charging behavior of layered oxides as cathode in sodium-ion batteries





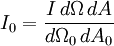 photons/(s·cm2·sr).
photons/(s·cm2·sr).
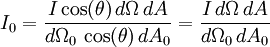 photons/(s·cm2·sr),
photons/(s·cm2·sr),


