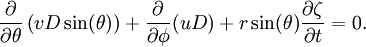To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Laplace's tidal equationsIn 1776, Pierre-Simon Laplace published a paper in which he analyzed the tides of a body of fluid with consideration as to the rotation of the body that fluid exists on. Product highlightGiven a sphere of radius r and angular velocity ω, covered in a fluid of depth D with velocity vector relative to the moving surface of the sphere (u, v), and with co-latitude and east longitude co-ordinates (θ, φ), and fluid displacement ζ, we have |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Laplace's_tidal_equations". A list of authors is available in Wikipedia. |