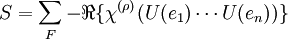To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Lattice gauge theoryIn physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized onto a lattice. Although most lattice gauge theories are not exactly solvable, they are of tremendous appeal because they can be studied by simulation on a computer. One hopes that, by performing simulations on larger and larger lattices, while making the lattice spacing smaller and smaller, that one will be able to recover the behaviour of the continuum theory. Product highlightIn lattice gauge theory, the spacetime is Wick rotated into Euclidean space, discretized and replaced by a lattice with lattice spacing equal to a. The quark fields are only defined at the elements of the lattice. There are problems with fermion doubling, though. See Wilson-Ginsparg action. Instead of a vector potential as in the continuum case, the gauge fields variables are defined on the links of the lattice and correspond to the parallel transport along the edge which takes on values in the Lie group. Hence to simulate QCD, for which the Lie group is SU(3), there is a 3 by 3 special unitary matrix defined on each link. The faces of the lattice are called plaquettes. The Yang-Mills action is rewritten using Wilson loops over plaquettes (it's simply a character evaluated over the composition of link variables around the plaquette) in such a way that the limit More precisely, we have a lattice with vertices, edges and faces. In lattice theory, the alternative terminology sites, links and plaquettes for vertices, edges and faces is often used. This reflects the origin of the field in solid state physics. While each edge happens to have no intrinsic orientation, to define the gauge variables, we assign an element of a compact Lie group G to each edge given an orientation for it called U. Basically, the assignment for an edge in a given orientation is the group inverse of the assignment to the same edge in the opposite orientation. Likewise, the plaquettes have no intrinsic orientations, but have to be temporarily given an orientation for computational purposes. Given a faithful irreducible representation ρ of G, the lattice Yang-Mills action is (the sum over all lattice sites of the (real component of the) Wilson loop). Here, χ is the character (trace) and the real component is redundant if ρ happens to be a real or pseudoreal representation. e1, ..., en are the n edges of the Wilson loop in sequence. The nice thing about being real is even if the orientation of a Wilson loop is flipped, its contribution to the action remains unchanged. There are many possible lattice Yang-Mills actions, depending on which Wilson loop is used in the above formula. The simplest is the Wilson action, in which the Wilson loop is just a plaquette. A disadvantage of the Wilson action is that the difference between it and the continuous action is proportional to the lattice spacing a. It is possible to use more complicated Wilson loops to form actions where this difference is proportional to a2, thus making computations more accurate. These are known as improved actions. To calculate a quantity (such as the mass of a particle) in lattice gauge theory, it should be calculated for every possible value of the gauge field on each link, and then averaged. In practice this is impossible. Instead the Monte Carlo method is used to estimate the quantity. Random configurations (values of the gauge fields) are generated with probabilities proportional to e − βS, where S is the lattice action for that configuration and β is related to the lattice spacing a. The quantity is calculated for each configuration. The true value of the quantity is then found by taking the average of the value from a large number of configurations. To find the value of the quantity in the continuous theory this is repeated for various values of a and extrapolated to a = 0. Lattice gauge theory is a particularly important tool for quantum chromodynamics (QCD). The discretized version of QCD is called Lattice QCD. QCD confinement has been shown in Monte Carlo simulations. Deconfinement at high temperature leads to the formation of a quark-gluon plasma. Lattice gauge theory has been shown to be exactly dual to spin foam models provided that the only Wilson loops appearing in the action are over plaquettes. See also
References and external links
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lattice_gauge_theory". A list of authors is available in Wikipedia. |





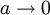 formally gives the original continuous action.
formally gives the original continuous action.