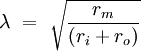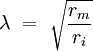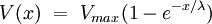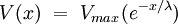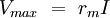Length constant

Length constant is a constant used in neurobiology signified by the Greek letter lambda (λ).

Additional recommended knowledge

Daily Sensitivity Test

Essential Laboratory Skills Guide

Safe Weighing Range Ensures Accurate Results

In an action potential (or in a passive spread of signal) in a neuron, the constant λ is

where r_m is the resistance across the membrane, r_i is the resistance inside the membrane, and r_o is the resistance outside the membrane. In calculation, the effects of r_o are negligible, so the equation becomes

The resistance across the membrane is a function of the number of open ion channels and the resistance inside the membrane is generally a function of the diameter of the axon. A large diameter is related to a lower r_i.

The length constant is used to describe the rise of potential difference across the membrane

The fall of voltage is described by

Where voltage is typically in millivolts, x is distance in millimeters, and λ is in millimeters.

V_max is defined as the maximum voltage attained in the action potential, where

where r_m is the resistance across the membrane and I is the current flow.

Setting for x= λ for the rise of voltage sets V(x) equal to .63 V_max. This means that the length constant is the distance at which 63% of V_max has been reached during the rise of voltage.

Setting for x= λ for the fall of voltage sets V(x) equal to .37 V_max, meaning that the length constant is the distance at which 37% of V_max has been reached during the fall of voltage.

The longer a length constant is, the bigger the effect of a potential (either an action potential or a current injected at the site) will have along the cell. A long length constant can result in spatial summation, or the algebraic summation of one potential with other potentials from other areas of the cell.

See also

• Time constant