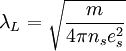To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
London equationsThe London equations relate the current to electromagnetic fields in and around a superconductor. Their purpose is to describe the magnetic field exclusion that is characteristic of a superconductor, and known as the Meissner effect. Product highlightThe first London equation relates the superconducting current to the electric field:
where ns is the density of Cooper pairs, and es and m are the charge and mass of a Cooper pair, respectively, which is simply twice the charge and mass of an electron. The second London equation relates the supercurrent to the magnetic field:
Writing the magnetic field in terms of the vector potential
where φ is an arbitrary phase.
Substituting this equation into the fourth of Maxwell's equations,
where is the London penetration depth. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "London_equations". A list of authors is available in Wikipedia. |





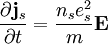 ,
,
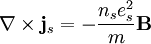 .
.
 , we find that the current is simply,
, we find that the current is simply,
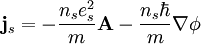 ,
,
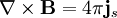 , and making use of Maxwell's third equation,
, and making use of Maxwell's third equation, 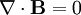 , we have
, we have
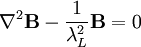 ,
,