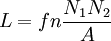To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Luminosity
Product highlight
In photometry and color imagingIn photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre. In Adobe Photoshop's imaging operations, luminosity is the term used incorrectly to refer to the luma component of a color image signal; that is, a weighted sum of the nonlinear red, green, and blue signals. It seems to be calculated with the Rec. 601 luma co-efficients (Rec. 601: Luma (Y’) = 0.299 R’ + 0.587 G’ + 0.114 B’). The "L" in HSL color space is sometimes said to stand for luminosity. "L" in this case is calculated as 1/2 (MAX + MIN), where MAX and MIN refer to the highest and lowest of the R'G'B' components to be converted into HSL color space. In astronomyIn astronomy, luminosity is the amount of energy a body radiates per unit time. The luminosity of stars is measured in two forms: apparent (counting visible light only) and bolometric (total radiant energy); a bolometer is an instrument that measures radiant energy over a wide band by absorption and measurement of heating. When not qualified, luminosity means bolometric luminosity, which is measured in the SI units watts, or in terms of solar luminosities, Luminosity is an intrinsic constant independent of distance, and is measured as absolute magnitude corresponding to apparent luminosity, or bolometric magnitude corresponding to bolometric luminosity. In contrast, apparent brightness is related to distance by an inverse square law. Visible brightness is usually measured by apparent magnitude, which is on a logarithmic scale. In measuring star brightnesses, visible luminosity (not total luminosity at all wave lengths), apparent magnitude (visible brightness), and distance are interrelated parameters. If you know two, you can determine the third. Since the sun's luminosity is the standard, comparing these parameters with the sun's apparent magnitude and distance is the easiest way to remember how to convert between them. Computing between brightness and luminosityImagine a point source of light of luminosity L that radiates equally in all directions. A hollow sphere centered on the point would have its entire interior surface illuminated. As the radius increases, the surface area will also increase, and the constant luminosity has more surface area to illuminate, leading to a decrease in observed brightness. where
For stars and other point sources of light, A = 4πr2 so where
It has been shown that the luminosity of a star L (assuming the star is a black body, which is a good approximation) is also related to temperature T and radius R of the star by the equation: where
Dividing by the luminosity of the sun
For stars on the main sequence, luminosity is also related to mass: It is easy to see that a star's luminosity, temperature, radius, and mass are all related. The magnitude of a star is a logarithmic scale of observed visible brightness. The apparent magnitude is the observed visible brightness from Earth, and the absolute magnitude is the apparent magnitude at a distance of 10 parsecs. Given a visible luminosity (not total luminosity), one can calculate the apparent magnitude of a star from a given distance: where
Or simplified, given msun = −26.73, distsun = 1.58 × 10−5 lyr:
Example:
Also you can calculate the luminosity given a distance and apparent magnitude:
Example: What is the luminosity of the star Sirius?
A bright star with bolometric magnitude −10 has a luminosity of 106 In scattering theory and accelerator physicsIn scattering theory and accelerator physics, luminosity is the number of particles per unit area per unit time times the opacity of the target, usually expressed in either the cgs units cm-2 s-1 or b-1 s-1. The integrated luminosity is the integral of the luminosity with respect to time. The luminosity is an important value to characterize the performance of an accelerator. Elementary relations for luminosityThe following relations hold
where
For an intersecting storage ring collider: where
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Luminosity". A list of authors is available in Wikipedia. |





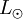 ; that is, how many times as much energy the object radiates than the
; that is, how many times as much energy the object radiates than the 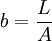
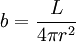
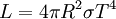
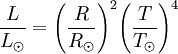 .
.
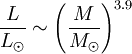
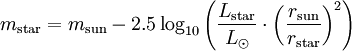
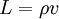 (if the target is perfectly opaque)
(if the target is perfectly opaque)
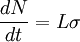
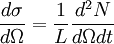
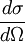 is the differential
is the differential