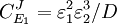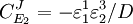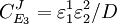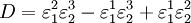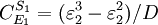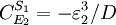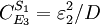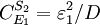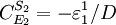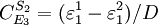To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Metabolic control analysis
MCA was originally developed to describe the control in metabolic pathways but was subsequently extended to describe signaling and genetic networks. MCA has sometimes also been referred to as Metabolic Control Theory but this terminology was rather strongly opposed by Henrik Kacser, one of the founders. More recent work [4] has shown that MCA can be mapped directly on to classical control theory and are as such equivalent. Biochemical systems theory [5] is a similar formalism, though with a rather different objectives. Both are evolutions of an earlier theoretical analysis by Joseph Higgins [6].
Product highlight
Control CoefficientsA control coefficient [7] [8][9] measures the relative steady state change in a system variable (e.g. fluxes or concentrations) in response to a relative change in a parameter (eg enzyme activity). The two main control coefficients are the flux and concentration control coefficients. Flux control coefficients are defined by:
and concentration control coefficients by:
Summation TheoremsThe flux control summation theorem was stated and proven by Kacser and Burns and it is one of the most fundamental discoveries of metabolic control analysis. The flux control summation theorem implies that metabolic fluxes are systemic properties and that their control is shared by all reactions in the system. When a single reaction changes its control of the flux this is compensated by changes in the control of the same flux by all other reactions.
Elasticity CoefficientsThe rate of a chemical reaction is influenced by many different factors, such as temperature, pH, reactant and product concentrations and other effectors. The degree to which these factors change the reaction rate is described by the elasticity coefficient.
Connectivity TheoremsThe connectivity theorems are specific relationships between elasticities and control coefficients. They are useful because they highlight the close relationship between the kinetic properties of individual reactions and the system properties of a pathway. Two basic sets of theorems exists, one for flux and another for concentrations. The concentration connectivity theorems are divided again depending on whether the system species Sn is different from the local species Sm.
Control EquationsIt is possible to combine the summation with the connectivity theorems to obtain closed expressions that relate the control coefficients to the elasticity coefficients. For example, consider the simplest non-trivial pathway: 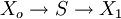 We assume that Xo and X1 are fixed boundary species so that the pathway can reach a steady state. Let the first step have a rate v1 and the second step v2. Focusing on the flux control coefficients, we can write one summation and one connectivity theorem for this simple pathway:
Using these two equations we can solve for the flux control coefficients to yield:
Using these equations we can look at some simple extreme behaviors. For example, let us assume that the first step is completely insensitive to its product, S, then
That is all the control (or sensitivity) is on the first step. This situation represents the classic rate-limiting step that is frequently mentioned in text books. The flux through the pathway is completely dependent on the first step. Under these conditions, no other step in the pathway can affect the flux. The effect is however dependent on the complete insensitivity of the first step to its product. Such a situation is likely to be rare in real pathways. In fact the classic rate limiting step has almost never been observed experimentally. Instead, a range of limitingness is observed, with some steps having more limitingness (control) than others. We can also derive the concentration control coefficients for the simple two step pathway:
An alternative approach to deriving the control equations is to consider the perturbations explicitly. Consider making a perturbation to E1 which changes the local rate v1. The effect on the steady-state to a small change in E1 is to increase the flux and concentration of S. We can express these changes locally by describing the change in v1 and v2 using the expressions: 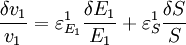
The local changes in rates are equal to the global changes in flux, J. In addition if we assume that the enzyme elasticity of v1 with respect to E1 is unity, then 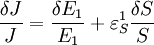
Dividing both sides by the fractional change in E1 and taking the limit
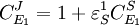
From these equations we can choose either to eliminate Three Step PathwayConsider the simple three step pathway:  where Xo and X1 are fixed boundary species, the control equations for this pathway can be derived in a similar manner to the simple two step pathway although it is somewhat more tedious.
where D the denominator is given by:
Note that every term in the numerator appears in the denominator, this ensures that the flux control coefficient summation theorem is satisfied. Likewise the concentration control coefficients can also be derived, for S1
And for S2
Note that the denominators remain the same as before and behave as a normalizing factor. References
Categories: Biochemistry methods | Metabolism |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Metabolic_control_analysis". A list of authors is available in Wikipedia. |





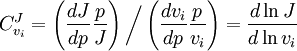
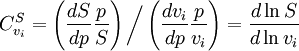
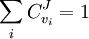
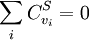
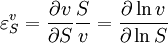
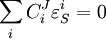
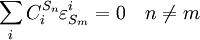
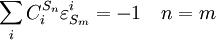
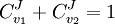
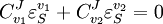
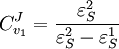
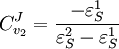
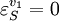 . In this case, the control coefficients reduce to:
. In this case, the control coefficients reduce to:
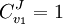
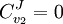
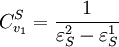
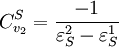
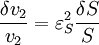
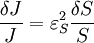
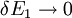 yields:
yields:
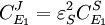
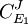 or
or 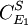 to yield the control equations given earlier. We can do the same kind of analysis for the second step to obtain the flux control coefficient for
to yield the control equations given earlier. We can do the same kind of analysis for the second step to obtain the flux control coefficient for