To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Method of imagesMethod of images (or mirror images) is a mathematical tool for solving differential equations in which the domain of the sought function is extended by the addition of its mirror image with respect to a symmetry hyperplane, with the purpose of facilitating the solution of the original problem. It is used in electrostatics to simply calculate or visualize the distribution of the electric field of a charge in the vicinity of the conducting surface. It is based on the fact that the tangential component of the electrical field to the surface of a conductor is zero, and that some field E with Product highlightThe method may also be used in magnetostatics for calculating the magnetic field of a magnet which is close to a superconducting surface. Here, the component of the magnetic field normal to the superconductor is zero.
A textbook example is an infinitely flat conducting surface (see Fig. 1). In this case the field distribution between the surface and a charge is the same as between this charge and another charge (imaginary charge), which is the mirror image of the real charge in respect to the surface but has the opposite sign. Evidently, in case of an electrical dipole, the vector of the mirrored dipole will have the opposite sign. Therefore, the force between the electrical charge or system of charges and the conducting surface is attractive. See also Method of image charges.
In case of magnet-superconductor pair (the superconductor here is ideal, to which the magnetic field does not penetrate), the mirror image of the magnet will have a magnetization vector which is mirrored but of the same sign (see Fig. 2). This can be thought as due to additional sign change upon mirroring of an axial vector which the magnetization is. The force between the magnet and the superconducting surface is therefore repulsive. Further reading
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Method_of_images". A list of authors is available in Wikipedia. |
- Accelrys Nanotechnology Consortium Adds Seven Members, Delivers First Computer-Aided Nanodesign Software Solution
- Perfect_conductor
- Instructional_Television_Fixed_Service
- Carbon nanotube computing? - Single-walled carbon nanotube composites show great promise for many things - including use as a material in 'unconventional' computing


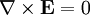 and
and 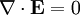 in some region is uniquely defined by its normal component over the surface which confines this region (the uniqueness theorem).
in some region is uniquely defined by its normal component over the surface which confines this region (the uniqueness theorem).





